Պրիզմա

 կոչվում է այն բազմանիստը, որի երկու նիստերը զուգահեռ հարթություններում ընկած հավասար բազմանկյուններ են, իսկ մնացած նիստերը զուգահեռագծեր են:

Զուգահեռ հարթություններում գտնվող հավասար նիստերը կոչվում են պրիզմայի հիմքեր, իսկ մնացած նիստերը՝ կողմնային նիստեր:

Հիմքերից կախված պրիզմաները լինում են եռանկյուն՝

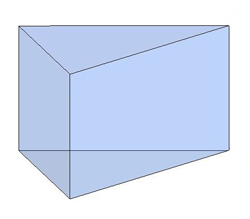
քառանկյուն՝

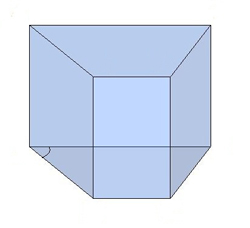
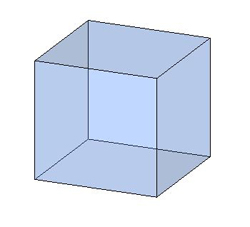
վեցանկյուն և այլն

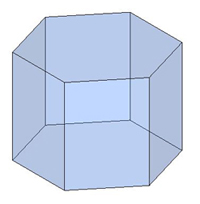
Եթե պրիզմայի կողմնային կողերը ուղղահայաց են հիմքերին, ապա այն կոչվում է ուղիղ պրիզմա: Այդպիսին են վերևի նկարներում ցուցադրված բոլոր պրիզմաները:

Հակառակ դեպքում, երբ կողմնային կողերը ուղղահայաց չեն հիմքերին, պրիզման կոչվում է թեք:

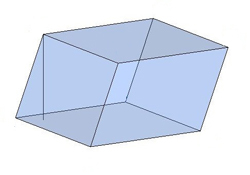
Պրիզման կոչվում է կանոնավոր, եթե նրա հիմքերը կանոնավոր բազմանկյուններ են:

n-անկյուն պրիզման ունի 3n կող, 2n գագաթ, n+2 նիստ, ընդ որում՝ նիստերից 2-ը հիմքերն են, իսկ n-ը՝ կողմնային նիստերը։

Առաջադրանքներ․

1)Քանի՞ նիստ ունի յոթանկյուն պրիզման:

n=7

7+2=9

2)Գտեք վեցանկյուն պրիզմայի կողերի, գագաթների, նիստերի թվերը:

6*3=18

6*2=12

6+2=8

3)Կարո՞ղ է պրիզմայի կողերի թիվը լինել՝
ա) 13
բ) 14
գ) 18

4)Ի՞նչ բազմանկյուն է պրիզմայի հիմքը, եթե պրիզման ունի 
ա) 18 կող

18:3=6
բ) 24 կող

24:3=8
գ) 9 նիստ

9-2=7

5)Կարո՞ղ է պրիզմայի նիստերի թիվը լինել՝
ա) 13 կարող է
բ) 14 կարող է
գ) 18 կարող է

6)Պրիզմայի գագաթների և կողերի թվերի գումարը 30 է: Քանի՞ նիստ,կող և գագաթ ունի այդ պրիզման:

2n+3n=30

30:5=n

n=6

6*2=12

6*3=18

Նիստ

6+2=8/