1)Նմա՞ն են ABC և A₁B₁C₁ եռանկյունները, եթե ∠A = A₁, ∠B = ∠B₁, ∠C=∠C₁, AB = 12 սմ, BC = 8 սմ, AC = 18 սմ, A₁B₁= 6 սմ, B₁C₁ = 4 սմ, A₁C₁ = 9 սմ: Նման են

2)ABC և A₁B₁C₁ եռանկյունները նման են, ընդ որում՝ ∠A = ∠A₁, ∠B = ∠B₁, BC = 14 դմ, AC = 9 դմ, B₁C₁= 7 դմ: Գտե՛ք A₁C₁-ը: A1 C1 =4.5 դմ:

3)ABC և KMN եռանկյունները նման են, ընդ որում՝ AB/MN = BC/NK = AC/MK: ABC և MNK եռանկյունների ո՞ր անկյուններն են համապատասխանաբար հավասար:
∠C=∠k, ∠A=∠M, ∠B= ∠N


4)ABC և A₁B₁C₁ նման եռանկյուններում AB = BC, A₁B₁ = B₁C₁ <BAC = 65o : Գտե՛ք <A₁B₁C₁ –ը: 50

5)ABC և A₁B₁C₁ եռանկյունները նման են, ընդ որում՝ <A = <A₁, BC = 15 սմ, B₁C₁ = 5 սմ: Գտե՛ք այդ եռանկյունների նմանության գործակիցը: 3

6)ABC և DEF եռանկյունները նման են։ <A = <D, <C = <F, EF = 14 սմ, DF = 20 սմ, BC = 21 սմ։ Գտեք AC–ն։

30

Առաջադրանքներ․

1)

2)

3)

4)

5)

6)

7)Գծեք AB, CD և EF վեկտորներն այնպես, որ՝

ա) AB, CD և EF վեկտորները լինեն համագիծ

բ) AB և EF վեկտորները լինեն համագիծ, իսկ AB և CD վեկտորները համագիծ չլինեն

1)Գտեք ABCD զուգահեռագծի D գագաթի կոորդինատները, եթե A(0, 0) B(5, 0) C(12,- 3):

12-5

(7;-3)

2)Գտեք A և B կետերի հեռավորությունը, եթե`

ա) A(2, 7), B(-2, 7),

dAB=√(-2-2)²+(7-7)² =√16=4

բ) A(-5, 1), B(-5, -7),

dAB=√(-5+5)²+(-7-1)²=√64=8

գ) A(-3, 0), B(0, 4),

dAB=√(0+3)²+(4-0)²=√25=5

դ) Α(0, 3), B(-4, 0):

dAB=(-4-0)²+(0-3)²=√25=5

3)Գտեք MNP եռանկյան պարագիծը, եթե M(4, 0), N(12, -2), P(5, -9):

dMN=√(12-4)²+(-2-0)²=√68

dMP=√(5-4)²+(-9-0)²=√82

dNP=√(5-12)²+(-9+2)²=√98

P=√68+√82+√98

4)Տրված են A(-2;1), B(1; 5), C(7;5), D(4;1) կետերը: Գտեք ABCD քառանկյան անկյունագծերը և պարագիծը:

AB=√(1+2)²+(5-1)²=√25=5

BC=√(7-1)²+(5-5)²=√36=6

DA=√(-2-4)²+(1-1)²=√36=6

CD=√(4-7)²+(1-5)²=√25=5

P=5+5+6+6=22

BD=√(4-1)²+(1-5)²=√25=5

AC=√(7+2)²+(5-1)²=√97

5)Ապացուցեք, որ A(1; 7), B(-1; — 1), C(-4; 2) գագաթներով ABC եռանկյունը ուղղանկյուն եռանկյուն է: Գտե՛ք այդ եռանկյան ներք– նաձիգին տարված միջնագիծը:

AB=√(-1-1)²+(-1-7)²=√68

BC=√(-4+1)²+(2+1)²=√18

AC=√(-4-1)²+(2-7)²=√50

√18+√50=√68

6)Գտե՛ք A(1; — 2), B(3; 5), C(8; 0) գագաթներով ABC հավասարասրուն եռանկյան մակերեսը:

AB=√(3-1)²+(5+2)²=√53

BC=√(8-3)²+(0-5)²=√50

AC=√(8-1)²+(0+2)²=√53

1)Հավասարասրուն եռանկյան սրունքը 17 սմ է, իսկ հիմքը՝ 16 սմ: Գտեք հիմքին տարված բարձրությունը:

Պատասխան՝ բարձրությունը 15 սմ է։

2)ա)Գտեք`հավասարակողմ եռանկյան բարձրությունը, եթե նրա կողմը 6 սմ է, 

Պատասխան՝ բարձրությունը 

33≈5.233≈5.2 սմ է։

բ) հավասարակողմ եռանկյան կողմը, եթե նրա բարձրությունը 4 սմ է:

Պատասխան՝ եռանկյան կողմը 833≈4.62383≈4.62 սմ է։

3)Քառակուսու անկյունագիծը 20 սմ է: Գտեք նրա կողմը։

Պատասխան՝ քառակուսու կողմը 102≈14.1410

4)Գտեք հավասարասրուն եռանկյան սրունքը և մակերեսը, եթե` ա) հիմքը 12 սմ է, իսկ հիմքին տարված բարձրությունը՝ 8 սմ, բ) հիմքը 18 սմ է, իսկ նրա հանդիպակաց անկյունը՝ 120°:

Պատասխան՝
Սրունքը՝ 63≈10.3963≈10.39 սմ,
Մակերեսը՝ 273≈46.76273≈46.76 սմ²

5)Ուղղանկյուն եռանկյան էջերն են a-ն և b-ն: Գտեք ներքնաձիգին տարված բարձրությունը, եթե`

ա) a = 5 b = 12 

բ) a = 12 b = 16 :

Պատասխան՝ h=9.6h

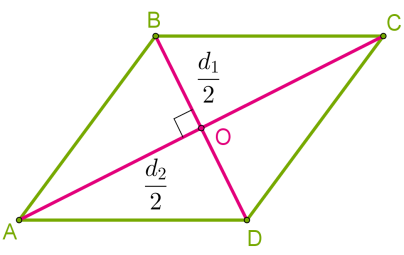
6)Գտեք շեղանկյան կողմը և մակերեսը, եթե նրա անկյունագծերը 10 սմ և 24 սմ են:

372

պատասխան՝

Եթե մակերեսը 72 սմ² է, ապա

• Շեղանկյան կողմը՝ մոտավորապես 10.95 սմ,
• Մակերեսը՝ 72 սմ²։

Սեղանի մակերեսը հավասար է հիմքերի կիսագումարի և բարձրության արտադրյալին:

S=1/2(AD+BC)BH

Քանի որ սեղանի հիմքերի կիսագումարը հավասար է դրա միջին գծին, ապա կարող ենք ասել,որ սեղանի մակերեսը հավասար է դրա միջին գծի ու բարձրության արտադրյալին.

S = MN ^. h

Առաջադրանքներ․

1)Սեղանի հիմքերը 12 սմ և 6 սմ են, բարձրությունը՝ 7 սմ: Գտեք սեղանի մակերեսը:

սեղանի մակերեսը 63 սմ² է:

2)Սեղանի հիմքերը 15 դմ և 5 դմ են, մակերեսը՝ 60 դմ² : Գտե՛ք սեղանի բարձրությունը:

սեղանի բարձրությունը 6 դմ է

3)Սեղանի միջին գիծը 13 սմ է, բարձրությունը`8 սմ: Գտեք սեղանի մակերեսը:

սեղանի մակերեսը 104 սմ² է։

4)35 սմ² մակերեսով սեղանի հիմքերը հարաբերում են ինչպես 2:3: Գտե՛ք եռանկյունների մակերեսները, որոնց տրոհվում է սեղանը իր անկյունագծով:

Սեղանի անկյունագծով տրոհված յուրաքանչյուր եռանկյունի ունի 17.5 սմ² մակերես։

5)Սեղանի բարձրությունը հավասար է փոքր հիմքին և երեք անգամ փոքր է մեծ հիմքից: Գտեք սեղանի մեծ հիմքը, եթե մակերեսը 72 դմ² է:

Սեղանի մեծ հիմքը մոտավորապես 11.4 դմ է։

6)CK-ն ABCD հավասարասրուն սեղանի C գագաթից AD մեծ հիմքին տարված բարձրությունն է: Գտեք սեղանի մակերեսը, եթե CK = 6 սմ, AK = 9 սմ:

Սեղանի մակերեսը 54 սմ² է։

1)Դիցուք՝ a-ն եռանկյան հիմքն է, h–ը՝ բարձրությունը, իսկ S-ը՝ մակերեսը: Գտեք՝

ա) S-ը, եթե a = 7 սմ, h = 11 սմ S=38.5S = 38.5S=38.5 սմ²

բ) h-ը, եթե a = 14 սմ, S = 37,8 սմ² h=5.4h = 5.4h=5.4 սմ

գ) a-ն, եթե S = h², h = 2 սմ: a=4a = 4a=4 սմ

2)ABC եռանկյան AB և BC կողմերը համապատասխանաբար 16 սմ և 22 սմ են: Գտեք BC կողմին տարված բարձրությունը, եթե AB կողմին տարված բարձրությունը 11 սմ է:

BC կողմին տարված բարձրությունը հավասար է 15.125 սմ:

3)Եռանկյան երկու կողմերն են 7,5 սմ և 3,2 սմ: Դրանցից մեծին տարված բարձրությունը 2,4 սմ է: Գտեք տրված կողմերից փոքրին տարված բարձրությունը:

Տրված կողմերից փոքրին տարված բարձրությունը 5.625 սմ է։

4)Գտեք ուղղանկյուն եռանկյան մակերեսը, եթե նրա էջերն են՝

ա) 4 սմ և 11 սմ, 22 սմ²

բ)12 սմ և 3 դմ: 180 սմ²

5)Ուղղանկյուն եռանկյան էջերից մեկը 14 սմ է, իսկ անկյուններից մեկը՝ 45°: Գտեք եռանկյան մակերեսը:

Եռանկյան մակերեսը 98 սմ² է։

6)Երկու եռանկյան բարձրությունները հավասար են, իսկ նրանցից մեկի հիմքը երկու անգամ փոքր է մյուսի հիմքից: Գտեք այդ եռանկյունների մակերեսների հարաբերությունը։

Եռանկյունների մակերեսների հարաբերությունը 1:2 է։

7)Գտեք 10 սմ ներքնաձիգով հավասարասրուն ուղղանկյուն եռանկյան մակերեսը

Եռանկյան մակերեսը 25 սմ² է։

8)ABCD ուղղանկյան BD անկյունագիծը 12 սմ է: B գագաթի հեռավորությունը AC ուղղից հավասար է 4 սմ: Գտեք ABC եռանկյան մակերեսը։

ABC-ի մակերեսը 24 սմ² է։

1)Գտե՛ք թիվ, որի քառակուսին հավասար է՝

ա)4

2

բ)100

10

գ)-6

չունի

դ)81

9

ե)-0,25

չունի

զ)0

0

է)0,09

0,3

ը)1,21

1,1

2)Հաշվե՛ք․

ա)2 + √1=3

բ)15 — √36=9

գ)√9 + √4=5

դ)√16 + √25=9

ե)√49 — √1=6

զ)√81 — √49=2

է)√100 — √36=4

ը)√144 — √121=1

թ)√0,36 + √0,49=1,3

3)Հաշվե՛ք․

ա)2 • √81=18

բ)1/3 • √100=1/3•10

գ)√4 • √0,25=1

դ)√0,16 • √9=1,2

ե)√0,27 : √3=0,27/3

զ)√49 : √0,01=0,7

է)√1/9 • √81=0,999…

ը)√0,36 : √1/36=0,6/1/36

թ)√1,69 : √0,0625=5,2

4)Հաշվե՛ք․

ա)(√2)² =2

բ)(√3)² =3

գ)(√13)² =13

դ)(√17)² =17

5)Հաշվե՛ք․

ա)

7/9

բ)

4/5

գ)

4/3

դ)

3/2

ե)

19/29

6)Համեմատե՛ք թվերը․

ա)√100 > √81

բ)√100 < √121

գ)√4 < 3

դ)1/5 < √0,25

ե)2 > √1/16

զ)9/5 > √4/49

է)√0,09 > √4/25

ը)√1/4 > 1/4

1)2, 3, -5 թվերից ո՞րն է հետևյալ համախմբի լուծում.

ա)

2; 3

բ)

3; -5

գ)

3; 2; -5

2)Լուծեք համախումբը.

ա)

3+3x-2<10-25x-3x

3-10-2<-3x-25x-3x

-9>-31x

x<9/31

8-2x-3>4x-7

-4x-2x>-8+3-7

-6x>-12

x<2

բ)

6y-2-1>4-5y

6y+5y>2+1+4

11y>7

y>7/11

6y-6<6y-6

y=R

գ)

3x+3>3x+3

լուծում չունի

2x-2<2x-2

լուծում չունի

դ)

4-4x>4-4x

լուծում չունի

5x+1<5x-1

լուծում չունի

ե)

6-3z-5z<-96+12+z

Զուգահեռագծի մակերեսը հավասար է նրա կողմի և նրան տարված բարձրության արտադրյալին:

Զուգահեռագծի բարձրությունը ուղղահայացն է, որը տարված է զուգահեռագծի կողմի ցանկացած կետից դեպի հանդիպակաց կողմը պարունակող ուղիղը:

Սովորաբար ուղղահայացը տանում են զուգահեռագծի գագաթից: Քանի որ զուգահեռագիծն ունի տարբեր երկարությամբ կողմերի երկու զույգ, ապա այն ունի տարբեր երկարությամբ երկու բարձրություն: 

BE բարձրությունը, որը տարված է երկու մեծ կողմերի միջև ավելի կարճ է, քան BF-ը, որը տարված է կարճ կողմերի միջև:  

Եթե a-ով նշանակել կողմը, իսկ h-ով բարձրությունը, ապա՝

Sզուգահեռագիծ=a⋅h

Շեղանկյան մակերեսը․

Շեղանկյան անկյունագծերը փոխուղղահայաց են և հատման կետով կիսվում են: Շեղանկյունը բաժանվում է չորս հավասար ուղղանկյուն եռանկյունների:

Շեղանկյան մակերեսի բանաձևը․

Sշեղանկյուն=d1⋅d2/2

Առաջադրանքներ․

1)Դիցուք՝ զուգահեռագծի հիմքը a-ն է, բարձրությունը՝ h-ը, իսկ մակերեսը՝ S-ը։ Գտեք՝

ա)S-ը, եթե a=15 սմ, h=12 սմ

15*12=180սմ²

բ)a-ն, եթե S=34 սմ² , h=8,5 սմ

34:8,5=4սմ

գ)h-ը, եթե S=162 սմ², a=9 սմ

162:9=18սմ

դ)a-ն, եթե h=1/2a, S=21a

21*1/2=42

a=42սմ

2)Զուգահեռագծի անկյունագիծը 13 սմ է և ուղղահայաց է զուգահեռագծի այն կողմին, որը 12 սմ է։ Գտեք զուգահեռագծի մակերեսը։

13*12=156

3)Զուգահեռագծի կից կողմերը հավասար են 12 սմ և 13 սմ, իսկ սուր անկյունը 30^o է։ Գտեք զուգահեռագծի մակերեսը։

12։2=6սմ

13*6սմ=78

4)Շեղանկյան կողմը 6 սմ է, իսկ անկյուններից մեկը՝ 150^o ։ Գտեք շեղանկյան մակերեսը։

6*3=18

5)Զուգահեռագծի կողմը 8,1 սմ է, իսկ 14 սմ-ի հավասար անկյունագիծը նրա հետ կազմում է 30^o անկյուն։ Գտեք զուգահեռագծի մակերեսը։

56,7

6)Դիցուք՝ a-ն և b-ն զուգահեռագծի կից կողմերն են, իսկ h₁-ը և h₂ -ը՝ բարձրությունները։ Գտեք՝

ա)h₂ -ը, եթե a=18 սմ, b=30 սմ, h₁ = 6 սմ, h₂ > h₁

S=a*h₂=b*h₁

a*h₂=b*h₁

h₂=30×6/18=10

h₂=b*h₁/a=30

բ)h₁ -ը, եթե a=10 սմ, b=15 սմ, h₂ =6 սմ, h₂ > h₁

15*h₁=10*h₂

h₁=10*h₂/15=10*6/15=4

h₁=4սմ

գ)h₁ -ը և h₂ -ը, եթե մակերեսը՝ S=54 սմ² , a=4,5 սմ, b=6 սմ

1)Մի քառակուսու կողմը k անգամ մեծ է մյուս քառակուսու կողմից: Գտե՛ք այդ քառակուսիների մակերեսների հարաբերությունը:

a²k²:a²=k²

2)Քառակուսաձև սենյակներից մեկի կողմը 2 անգամ փոքր է մյուսի կողմից: Գտե՛ք փոքր սենյակի մակերեսը, եթե մեծի մակերեսը 36 մ է:

6:2=3

3×3=9

3)Խոհանոցի պատը երեսապատված է 15 սմ կողմով քառակուսաձև 120 սալիկով: Քանի՞ ուղղանկյունաձև նոր սալիկ է պետք նույն պատը երեսապատելու համար, եթե նոր սալիկների կից կողմերը 10 սմ և 20 սմ են:

15*15=225

120*225=27000

10*20=200

27000:200=135

4)Գտե՛ք 54 սմ պարագծով ուղղանկյան մակերեսը, եթե՝
ա) կից կողմերից մեկը մյուսից մեծ է 3 սմ–ով,

54-6=48

48:4=12

12+3=15

15*12=180

բ) կից կողմերը հարաբերում են, ինչպես 4 : 5,

54:18=3

3*4=12

3*5=15

15*12=180
գ) կողմերից մեկը (b + 17) սմ է:

2a+2b+34=54

54-34=20

20:2=10

(10-b)(b+17)