Առաջադրանքներ․

1.Որքա՞ն է ներգծյալ անկյունը, որը հենված է 28° աստիճանային չափով աղեղի վրա:

Ներգծյալ անկյունը, որը հենված է աղեղի վրա, հավասար է այդ աղեղի կեսին:

Պատասխան: Ներգծյալ անկյունը կլինի 28° / 2 = 14°:

2.Դիցուք BAC անկյունը 35° է: Որքա՞ն է BnC աղեղի աստիճանային չափը։

Բացատրություն. Երբ BAC անկյունը տրվում է, ապա աղեղի չափը հաշվարկելու համար պետք է գիտակցել, որ Բաքու ամեն արշավելու դեպքում աղեղը կլինի երկակի անկյան չափը:

Պատասխան: Աղեղի աստիճանային չափը կլինի 35° × 2 = 70°:

3.Գտիր ASB անկյունը, եթե ASB աղեղի աստիճանային չափը 268° է:

Ներգծյալ անկյունը հավասար է աղեղի կեսին:

Պատասխան: ASB անկյունը կլինի 268° / 2 = 134°:

4.Գտիր BOC և BAC անկյունները, եթե ∪AB=130° ∪AC=150° ։

Այսպիսի հարցի լուծման համար անհրաժեշտ է օգտագործել հարաբերությունները, երբ երկու աղեղները միևնույն կենտրոնում է։

1. BOC անկյունը որոշելու համար՝ պետք է հաշվի առնել, որ կենտրոնային անկյունը հավասար է աղեղի չափին: Իսկ BAC անկյունը կլինի այդ աղեղի կեսը:

Պատասխան. BOC անկյունը կլինի 130°: BAC անկյունը՝ 130° / 2 = 65°:

5.Հաշվիր AOB եռանկյան անկյունները, եթե ∪AB=100°։

Եթե համարը տալիս է ամբողջական փոփոխություն միայն մեկ աստիճանում:

Պատասխան. AOB եռանկյակի երեք անկյունները գումարով պետք է հասնեն 180°: Եթե ∪AB = 100°, ապա մնացած երկու անկյունները կլինեն՝

AOB անկյունը=180°−100°=80°\text{AOB անկյունը} = 180° — 100° = 80°AOB անկյունը=180°−100°=80°

6. ACB աղեղի աստիճանային չափը 260° է: Գտիր AOB և ACB անկյունները:

Պատասխան. ACB աղեղի չափը 260° է:

• ACB անկյունը կլինի 260° / 2 = 130° (այս անկյունը կապվում է ուղիղ շրջադարձի միջոցով):
• AOB անկյունը կլինի մնացած մասը՝ 180° — 130° = 50°:

Պրիզմա

 կոչվում է այն բազմանիստը, որի երկու նիստերը զուգահեռ հարթություններում ընկած հավասար բազմանկյուններ են, իսկ մնացած նիստերը զուգահեռագծեր են:

Զուգահեռ հարթություններում գտնվող հավասար նիստերը կոչվում են պրիզմայի հիմքեր, իսկ մնացած նիստերը՝ կողմնային նիստեր:

Հիմքերից կախված պրիզմաները լինում են եռանկյուն՝

քառանկյուն՝

վեցանկյուն և այլն

Եթե պրիզմայի կողմնային կողերը ուղղահայաց են հիմքերին, ապա այն կոչվում է ուղիղ պրիզմա: Այդպիսին են վերևի նկարներում ցուցադրված բոլոր պրիզմաները:

Հակառակ դեպքում, երբ կողմնային կողերը ուղղահայաց չեն հիմքերին, պրիզման կոչվում է թեք:

Պրիզման կոչվում է կանոնավոր, եթե նրա հիմքերը կանոնավոր բազմանկյուններ են:

n-անկյուն պրիզման ունի 3n կող, 2n գագաթ, n+2 նիստ, ընդ որում՝ նիստերից 2-ը հիմքերն են, իսկ n-ը՝ կողմնային նիստերը։

Առաջադրանքներ․

1)Քանի՞ նիստ ունի յոթանկյուն պրիզման:

n=7

7+2=9

2)Գտեք վեցանկյուն պրիզմայի կողերի, գագաթների, նիստերի թվերը:

6*3=18

6*2=12

6+2=8

3)Կարո՞ղ է պրիզմայի կողերի թիվը լինել՝
ա) 13
բ) 14
գ) 18

4)Ի՞նչ բազմանկյուն է պրիզմայի հիմքը, եթե պրիզման ունի 
ա) 18 կող

18:3=6
բ) 24 կող

24:3=8
գ) 9 նիստ

9-2=7

5)Կարո՞ղ է պրիզմայի նիստերի թիվը լինել՝
ա) 13 կարող է
բ) 14 կարող է
գ) 18 կարող է

6)Պրիզմայի գագաթների և կողերի թվերի գումարը 30 է: Քանի՞ նիստ,կող և գագաթ ունի այդ պրիզման:

2n+3n=30

30:5=n

n=6

6*2=12

6*3=18

Նիստ

6+2=8/

Բուրգի մասին դուք նախնական տեղեկություններ ունեք: Հին աշխարհի յոթ հրաշալիքներից են Եգիպտական բուրգերը:

Բուրգն այն բազմանիստն է, որի նիստերից մեկը բազմանկյուն է, իսկ մյուս բոլոր նիստերն ընդհանուր գագաթով եռանկյուններ են:

Բազմանկյունը կոչվում է բուրգի հիմք, իսկ նույն գագաթով եռանկյունները՝ կողմնային նիստեր: Բուրգի գագաթից հիմքի հարթությանն իջեցված ուղղահայացը կոչվում է բուրգի բարձրություն:

Եթե բուրգի հիմքը n-անկյուն բազմանկյուն է, ապա բուրգն անվանում են n-անկյուն բուրգ:

n-անկյուն բուրգն ունի 2n կող, որոնցից n-ը հիմքի կողերն են, իսկ n-ը՝ կողմնային կողերը:

n-անկյուն բուրգն ունի n+1 նիստ, որոնցից 1-ը հիմքն է, իսկ n-ը՝ կողմնային նիստերը:

n-անկյուն բուրգն ունի n+1 գագաթ, որոնցից 1-ը բուրգի գագաթն է, իսկ n-ը՝ հիմքի գագաթներն են:

Առաջադրանքներ․

1)Բերված մարմիններից ո՞րն է բուրգը:

սա է բուրգ։

2)Քանի՞ նիստ ունի իննանկյուն բուրգը:

10 նիստ ունի։

3)Գտեք 8-անկյուն բուրգի կողերի, նիստերի և գագաթների թվերը։

16 նիստ 1 գագաթ։

4)Գտիր 45-անկյուն բուրգի կողերի թիվը:

90 կողմ։

5)Ինչպե՞ս է կոչվում բուրգը, եթե այն ունի՝

ա)6 նիստ

բազմանկյուն

բ)10 գագաթ

գ)12 կող

կողմնային կողմեր

6)Կարո՞ղ է լինել այնպիսի բուրգ, որն ունի՝

ա)9 նիստ

այո

բ)9 կող

ոչ

7)Քառանկյուն բուրգի հիմքը 64 սմ պարագծով քառակուսի է, իսկ կողմնային նիստերը հավասարակողմ եռանկյուններ են։Գտեք բուրգի կողմնային կողերը։

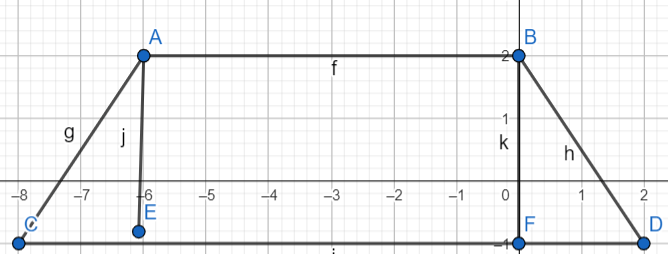
1)Ո՞ր պատկերն է կոչվում բազմանկյուն։Գծե՛ք բազմանկյուն, ցույց տվեք գագաթը,կողմերը։

բոլոր հատվածները չեկ գտնվում մի ուղիղի վրա, իսկ ոչ կից հատվածները ընդանուր կետ չունեն։ Այդպիսի պատակերը կողվում է բազմանկյուն։ A, B, C …… E, F կետերը կոչվում են բազմանկյան գագաթներ։ AB, BC …… EF հատվածները կոչվում են բազմանկյան կողմեր։

2)Ո՞ր բազմանկյուններն են կոչվում ուռուցիկ։Գծե՛ք ուռուցիկ և ոչ ուռուցիկ բազմանկյուններ, ցույց տվեք անկյունները։

Բազմանկյունը կոչվումէ ուռուցիկ եթե այն ընկած է իր ցանկացաց երկու հարևան գագաթներով անցնող ուղիղի մի կողմում

3)Գրեք ուռուցիկ n-անկյան անկյունների գումարի հաշվման բանաձևը։

(n — 2) x 180:

4)Ինչի՞ է հավասար ուռուցիկ հնգանկյան անկյունների գումարը։

(5 — 2) x 180 = 540

5)Սահմանեք զուգահեռագիծը։ Զուգահեռագիծը արդյո՞ք ուռուցիկ քառանկյուն է։

Զուգահեռագիծ կոչվում է այն քառանկյունը, որի հանդիպակած կողմերը զույգ առ զույգ զուգահեռ են։

Զուգահեռագիծը ուռոցիք քառանկյուն է։

6)Ի՞նչ է եռանկյան միջին գիծը։ Գծե՛ք եռանկյուն, տարե՛ք միջին գիծը և գրեք միջին գծի հաշվման

բանաձևը։ ։

Եռանկյան միջին գիծը եռանկյան երկու կողմերի միջնակետերը միացնող հատվածն է։ Ամեն եռանկյուն ունի երեք միջին գիծ։

DE = AC/2

7)Ո՞ր քառանկյունն է կոչվում սեղան։ Ինչպե՞ս են կոչվում սեղանի կողմերը։

Սեղան կոչվում է այն քառանկյունը, որի երկու կողմերը զուգահեռ են, իսկ մյուս երկու կողմերը զուգահեռ չեն։Զուգահեռ կողմերը կոչվումեն սեղանի հիմքեր, իսկ երկու մյուս կողմերը ՛ սրունքներ:

8)Ո՞ր սեղանն է կոչվում հավասարասրուն, ո՞րը՝ ուղղանկյուն։ Գծեք օրինակներ։

Սեղանը կոչվում է հավասարասրուն եթե նրա սրունքները հավասար են։

Սեղանը, որի որևէ անկյունն ուղիղ է կոչվում է ուղղանկյուն սեղան։

9)Ի՞նչ է սեղանի միջին գիծը։ Գծե՛ք սեղան, տարե՛ք միջին գիծը և գրեք միջին գծի հաշվման բանաձևը։

Սեղանի միջին գիծը զուգահեռ է հիմքերին և հավասար է նրանց կիսագումարին։

BC + AD/2

10)Ո՞ր քառանկյունն է կոչվում ուղղանկյուն։

ուղանկյուն կոչվում է այն զուգահեռագիծը, որի բոլոր անկյուները ուղիղ են։

11)Ո՞ր քառանկյունն է կոչվում շեղանկյուն։

Շեղանկյուն կոչվում է այն զուգահեռագիծը, որի բոլոր կողմերը հավասար են։

12)Ո՞ր քառանկյունն է կոչվում քառակուսի։

քառակուսի կոչվում է այն ուղանկյունը, որի բոլոր կողմերը հավասար են։

Առաջադրանքներ․

1)Ուղղանկյան անկյունագծերի հատման կետի հեռավորությունը մեծ կողմից 4սմ է, իսկ փոքր կողմից՝ 6սմ։ Գտեք ուղղանկյան պարագիծը։

2)Գտեք ABCD ուղղանկյան պարագիծը, եթե A անկյան կիսորդը տրոհում է՝

BC=45,6+7,85=53, AB=EC=7,85 P=53,45+7j8=61,3

ա)BC կողմը 45,6սմ և 7,85սմ երկարությամբ հատվածների

բ)DC կողմը 2,7դմ և 4,5դմ երկարությամբ հատվածների

3)ABCD ուղղանկյան անկյունագծերը հատվում են O կետում։ Գտեք AOB եռանկյան պարագիծը, եթե <CAD = 30^o, AC = 12սմ։

Լրացուցիչ աշխատանք (տանը).

1)Ուղղանկյան կից կողմերից մեկը 10սմ է, իսկ մյուսը՝ 13սմ։ Գտե՛ք ուղղանկյան պարագիծը։

2)ABCD ուղղանկյան AB կողմը 6սմ է, իսկ BDA անկյունը՝ 30^o։ Գտե՛ք AC անկյունագիծը։

3)ABCD ուղղանկյան անկյունագծերը հատվում են O կետում, E-ն AB կողմի միջնակետն է, <BAC = 50^o։ Գտեք <AOE-ն։

1)Հավասարասրուն սեղանի սրունքը հավասար է փոքր հիմքին և մեծ հիմքից փոքր է երկու անգամ։ Գտեք սեղանի պարագիծը, եթե փոքր հիմքը 7 է։

BA=CD=3սմ
BC||AD
P=AB+BC+CD+AD=3+7+3+21=34սմ
Պատ.՝34սմ

2)ABCD հավասարասրուն սեղանի C գագաթից AD մեծ հիմքին տարված է CK ուղղահայացը։ Գտե՛ք սեղանի հիմքերը, եթե դրանց գումարը 18սմ է, իսկ KD=1սմ։

18-2=16

16:2=8

18-8=10

3)Հավասարասրուն սեղանի անկյունագիծը կիսում է դրա բութ անկյունը։ Սեղանի փոքր հիմքը 3սմ է, իսկ պարագիծը՝ 42սմ։ Գտե՛ք սեղանի մեծ հիմքը։

Լրացուցիչ աշխատանք (տանը).

1)Գտե՛ք 13սմ և 19սմ հիմքերով սեղանի միջին գիծը։

2)Հավասարասրուն սեղանի մեծ հիմքը երկու անգամ մեծ է փոքր հիմքից։Սեղանի անկյունագիծը դրա սուր անկյունը բաժանում է հավասար մասերի։ Գտե՛ք սեղանի փոքր հիմքը, եթե սեղանի պարագիծը 60սմ է։

3)Գտե՛ք սեղանի հիմքերի երկարությունները, եթե դրանց տարբերությունը 7սմ է, իսկ սեղանի միջին գիծը 12սմ է։

1.Հավասարասրուն եռանկյան պարագիծը հավասար է 1մ-ի, իսկ հիմքը՝ 0,4 մ-ի: Գտեք սրունքի երկարությունը։

1 մ-100սմ

0,4 մ-40 սմ

100-40=60 սմ

60:2=30 սմ

Սրունքի երկարությունը-0,3 մ, կամ 30 սմ

2.Հավասարասրուն եռանկյան արտաքին անկյուններից մեկի մեծությունը 120^o է։ Գտեք այդ եռանկյան անկյունների մեծությունները։

3.<3-ը երկու անգամ մեծ է <1 -ից : Գտնել <2-ը և <4-ը։

<3=120°, <1=60°

<3=<2 խաչադիր անկյուններ

<1=<4 խաչադիր անկյիւններ

<1=60°,<2=120°,<3=120°,<4=60°

Բոլոր գծագրերի համար հաշվել <DBA-ն։

1․Քանի որ ABD հացասարաչափ անկյուն է դրա համար անում ենք ՝ 70 x2=140
180-140=40

2. 180-70=110 աստիճան
3․Հակադիր անկյունները իրար հավասար են այսինքն՝
70 աստիճան

4․
40+40=80
180-80=100
100:2=50
ABD=90

5.
50×2=100
180-100=80
80:2=40
DBA=90

6.
30+30=60
180-60=120
120:2=60
DBA=60

7. 120

8. 90

9. 55


10. 20

1.Քանի՞ ուղիղ և քանի՞ հատված ես տեսնում նկարի վրա։

Ուղիղներ-c, h,

Ճառագայթներ-CD, AB, FE, HG

2.AC հատվածի   երկարությունը 4 սմ է,  BC հատվածինը՝ 10 սմ : Գտիր  AB  հատվածի   երկարությունը:

Լուծում

1. AB=AC+BC=10+4=14սմ

3.AB հատվածի   երկարությունը 27 սմ ,  AC հատվածը՝ 8 սմ : Գտիր  CB   հատվածի   երկարությունը:

Լուծում

1. CB=AB-AC=27-8=19սմ

4.Քանի՞ հատված ես տեսնում նկարի վրա։

8-CD,ED,DF,EF,AB,CB,CF,FB

5.AB հատվածի երկարությունը 50սմ է։ Այդ հատվածի վրա վերցված են M և N կետերը այնպես, որ AM=23սմ, NB=21սմ։ Գտնել MN հատվածի երկարությունը։

1)Նշե’ք որևէ չորս A, B, C, D, կետեր: A և D կետերը միացրեք բեկյալ գծով, որը անցնում է B և C կետերով: Որոշել բեկյալի երկարությունը:

AB=5սմ

BC=4սմ

CD=5սմ

AD-?

5+5+4=14

2)Գտնել ABCDE բեկյալի երկարությունը, եթե AB=11սմ, BC=5 սմ, CD=8 սմ, DE=14 սմ:

11+5+8+14=38

3)Գտնել ABCD բեկյալի երկարությունը՝ արտահայտված սանտիմետրով։ Եթե AB=20դմ, BC=50 դմ, CD =80դմ։

20+50+80=150դմ

150×10=1500սմ

4)Բեկյալի օղակների երկարություններն են 5 սմ, 6սմ և 8 սմ։ Գտեք այդ բեկյալի երկարությունը։

5+6+8=19

5)A-ից B գնալու համար նույն արագությամբ շարժվող հետիոտներից առաջինն ընտրեց կապույտ ճանապարհը, երկրորդը՝ կանաչ ճանապարհը, երրորդը՝ դեղին ճանապարհը։ Ի՞նչ հերթականությամբ նրանք տեղ հասան։

Դեղին, կանաչ, կապույտ,