1)Զուգահեռագծի կից կողմերը 10 սմ և 14 սմ են, անկյուններից մեկը` 60°։ Գտե՛ք զուգահեռագծի մակերեսը:
70√3 սմ²
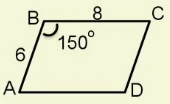
2)Զուգահեռագծի կից կողմերը 6 սմ և 12 սմ են, անկյուններից մեկը՝ 150°։ Գտե՛ք զուգահեռագծի մակերեսը:
36 սմ²
3)135√2 դմ2 մակերեսով զուգահեռագծի կից կողմերը 15 դմ և 18 դմ են: Գտե՛ք զուգահեռագծի անկյունները:
45° և 135°
4)Զուգահեռագծի կողմերից մեկը 2 սմ-ով մեծ է մյուսից, իսկ դրանց կազմած անկյունը 60° է: Գտե՛ք զուգահեռագծի կողմերը, եթե դրա մակերեսը 24√3 սմ2 է:
6 սմ 8 սմ
5)Գտեք շեղանկյան մակերեսը, եթե նրա կողմը հավասար է 12 սմ, իսկ անկյունը`60o :
72√3 սմ²
6)Գտեք շեղանկյան կողմը, եթե նրա մակերեսը հավասար է 8√2 սմ2, իսկ անկյունը` 45o։
4 սմ
7)322√2 սմ2 մակերեսով շեղանկյան անկյուններից մեկը 45° է: Գտե՛ք շեղանկյան կողմը:
2√161 սմ