1)Տրված է f(x) = √(x — 2) + 1 ֆունկցիան: Գտե՛ք ֆունկցիայի արժեքը ա) 6, բ) 2, գ) 4 կետում:

3, 1, √2+1

2)Տրված է f(x) = √(x + 1) ֆունկցիան: Գտե՛ք ֆունկցիայի արժեքը ա) 0, բ) -1, գ) 8 կետում:

1, 0, 3

3)Տրված է f(x) = -√(2x) ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 3, բ) —1, գ) –10 արժեքը:

լուծում չունի, 0,5, 50
4)Տրված է f(x) = -√(x+6)ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) −1, բ) 0, գ) −4, դ) 3 արժեքը:

-5, -6, 10, լուծում չունի

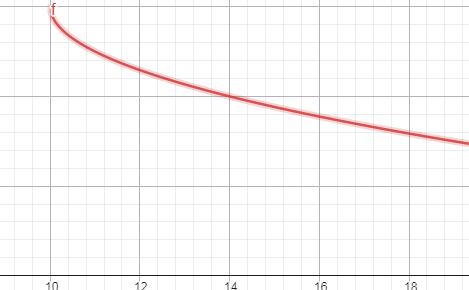
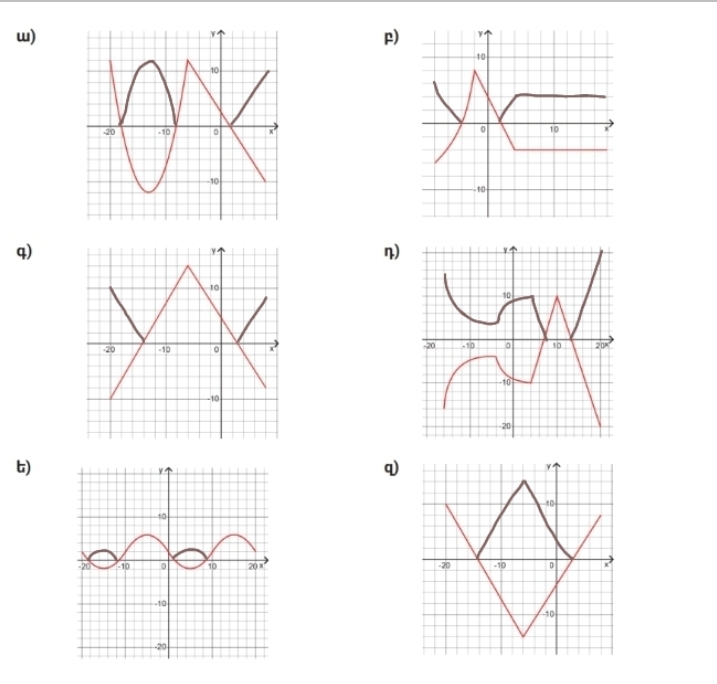
5)Նկարում պատկերված է y =√(x — x₀) + y₀ ֆունկցիայի գրաֆիկը: Գտե՛ք x₀ և y₀ թվերը.

x=0 y=6

x=4, y=0

x=6 y=8

x=-12 y=6

x=-6 y=-14

x=6 y=-4

6)Կառուցե՛ք ֆունկցիայի գրաֆիկը.

ա) y = √(x) — 2

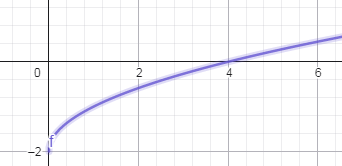
բ) y = √(x) + 3

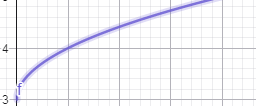
գ) y = √(x + 5)

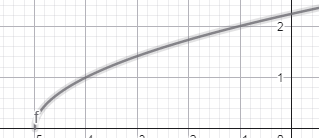
դ) y = √(x — 3) + 5

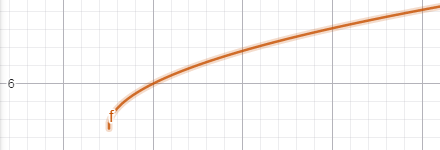
ե) y = √(x + 2) — 8

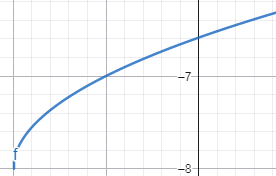
զ) y = — √(x — 10) + 6

1)Տրված է f(x) = |x — 1| ֆունկցիան: Գտե՛ք ֆունկցիայի արժեքը ա) 2, բ) 0, գ) –2 կետում:

1, 1, 3

2)Տրված է f(x) = 2|x + 3| ֆունկցիան: Գտե՛ք ֆունկցիայի արժեքը ա) – 5, բ) 1, գ) –3 կետում:

4, 8, 0

3)Տրված է f(x) = |x — 4| ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 2, բ) 0, գ) -4, դ) 7 արժեքը:

6, 4, լուծում չունի, {11,3}

4)Տրված է f(x) = |x + 9| ֆունկցիան: Ո՞ր կետերում է ֆունկցիան ընդունում ա) 1, բ) 8, գ) -1, դ) 5 արժեքը:

{-10,-8} {-171,-1}, լուծում չունի, {-14, -4}

5)Նկարում պատկերված է y = f(x) ֆունկցիայի գրաֆիկը: Գծե՛ք y = |f(x)| ֆունկցիայի գրաֆիկը.

1)Տրված է 1, 3, 9, 27, … երկրաչափական պրոգրեսիան։ Գտեք նրա հայտարարը և հինգերորդ, վեցերորդ ու յոթերորդ անդամները:

q=3

81, 486, 1458

2)Հաջորդականությունն արդյոք երկրաչափական պրոգրեսիա՞ է.
ա) 1, 8, 15, 21, 26, Ոչ;
բ) 4, 2, 1, 0,5, 0,25, Այո;
գ) -2, 2, -2, 2, -2, Այո;
դ) 0, 4, 16, 64, 256, Ոչ:

3)Գտեք a_n երկրաչափական պրոգրեսիայի առաջին չորս անդամները, եթե a₁ = 2, q = 0,25 :

2, 0.5, 0.125, 0,81224

4)Տրված է a_n երկրաչափական պրոգրեսիան։ Հաշվեք.
ա)a₃ — ը, եթե a₁= 0,5, q = — 2;

2

բ)a₄ — ը, եթե a₁ = -2, q = 3;

-54

գ) a₃ — ը և q — ն, եթե a₁ = 3, a₂ = 4;

4/3 16/3

դ) a₃ — ը և q — ն, եթե a₁ = — 4, a₂ = 6

-1.5 -9

5)Տրված են երկրաչափական պրոգրեսիայի երեք իրար հաջորդող անդամներ.
ա) 7, x, 63։ Գտեք x — ը, եթե x > 0 :

21

բ) 2, x, 18։ Գտեք x — ը, եթե x < 0 :

-6

գ) 3,2; x; 0,2։ Գտեք x — ը ։

0.8

1)Արտահայտությունն արտահայտե´ք a₁-ով ու d-ով.
ա) a₅ + a₁₀

a1+4d+a1+9d=2a1+13d
բ) a₃ + 2a₇

a1+2d+2a1+12d=3a1+14d
գ) a₇ + a₈ — 2a₆

a1+6d+a1+7d-2a1-10d=3d
դ) a₁₅ + a₁₇ — 2a₁₆

a1+14d+a1+16d-2a1-30d=0

2){a_n} թվաբանական պրոգրեսիայում գտեք
ա) a₂ և d-ն, եթե a₁ = 5, a₃ = 13 ;

9 4

բ) a₁ և d-ն, եթե a₂ = 3 , a₁₀ = 19 ;

1 2

գ) a₂ և d-ն, եթե a₁₂ = — 2 , a₃ = 7 ;

-1
դ) a₁₀₁ և d-ն, եթե a₁₂ = 20,5 ; a₇ = 10, 5 :

2 

3)Տրված է {a_n} թվաբանական պրոգրեսիան։ Հաշվեք․
ա) S₂₀ — ը, եթե a₁ = 1 , a₂₀ = 20 ;\

s20=20*1+20/2=210
բ) S₁₃, եթե a₁ = 17, a₁₃ = 13 ;

s13=13*17+13/2=195
գ) S₃₀, եթե a₁ = — 10 a₃₀ = 20 ;

s30=30*-10+20/2=150
դ) S₁₇, եթե a₁ = 11, a₁₇ = 19 :

s17=17*11+19/2=255

Առաջադրանքներ․

1)Գտե՛ք օրինաչափությունը և հաջորդականության հաջորդ անդամը.
ա) 1, 11, 111, 1111, 11111,
բ) 1,-2, 3, 4, 5, -6, 7,
գ) 1, 0, 1, 0, 1, 0, 1, 0,
դ) 1, 2, 3, 1, 2, 3, 1, 2,
ե) 1, 2, 4, 5, 7, 8, 10, 11, 12,
զ) 1, 2, 2, 3, 3, 3, 4, 4:

2)Գրե՛ք բանաձևով տրված հաջորդականության առաջին 5 անդամը.
ա)a_n = 2n + 1

3, 5, 7, 9, 11
բ)a_n = 7(n — 2)

-7, 0, 7, 14, 21
գ)a_n = — 4n + 2

-2, -6, -10, -14, -18
դ)a_n = 1.5n + 2

3.5, 5, 6.5, 8, 9.5
ե)a_n = 3ⁿ

3, 9, 27, 81, 243
զ)a_n = 6 * 2^{n — 1}

0, 12, 36, 84, 180
3)Հաշվե՛ք n-րդ անդամի բանաձևով տրված հաջորդականության երրորդ և չորրորդ անդամները.
ա) a_n = (n — 3)⁵

0, 1
բ) b_n = (n + 1)^{n — 4}

0.25, 1
գ) e_n = (- 1)ⁿ * n

-3, -4

4)Տրված է հաջորդականության n-րդ անդամի բանաձևը.
ա) a_n = 3n — 1 Գտեք a₁, a₂, a₅ , a₁₀₀ -ը։

2, 5, 14, 299
բ)a_n = 3 + 2(n — 1) Գտեք a₁, a₂, a₁₂ , a₃₀ -ը։

3, 5, 25, 61

5)Գտեք ընդհանուր անդամի բանաձևով տրված հաջորդականության առաջին վեց անդամների գումարը.
ա) a_n = 3n + 2

75
բ) a_n = (- 1)ⁿ * n

3

1)Փոփոխականի փոխարինմամբ ստացե՛ք քառակուսային հավասարում.
ա) (x + 2)² + 5(x + 2) — 3 = 0
բ) (x — 4)² — 3(x — 4) + 1 = 0
գ) 2(x — 3)² — (x — 3) + 5 = 0
դ) 2(x + 7)² — 4(x + 7) — 1 = 0

a2+5a-3=0

a2-3a+1=0

2a2-a+5=0

2a2-4a-1=0

2)Փոփոխականի փոխարինմամբ լուծե՛ք հավասարումը.
ա) (x — 4)² + 6(x — 4) + 5 = 0

y2+6y+5=0

y=-1 y=-5

xϵ{-1;3}
բ) (x + 1)² — 7(x + 1) — 18 = 0

y2-7y-18=0

y=9 y=-2

xϵ{-3;8}
գ) (x — 1)² + 8(x — 1) + 12 = 0

y2+8y+12=0

y=-2 y=-6

xϵ{-5;-1}
դ) (4z + 3)² — (4z + 3) — 2 = 0

y2-y-2=0

y=2 y=-1

zϵ{-1;-1/4}

3)Փոփոխականի փոխարինմամբ ստացե՛ք քառակուսային հավասարում.
ա) a⁴ + 5a² — 7 = 0

y2+5y-7=0
բ) 4x⁴ + 9x² — 1 = 0

4y2+9y-1=0
գ) 5x⁴ + 9x²— 12 = 0

5y2+9y-12=0
դ) -2b⁴ + 7b² + 1 = 0

-2y2+7y+1=0

1)Լուծե՛ք ռացիոնալ հավասարումը.

x=0

x=2

x=3

x=5 x=-6

x=1

x=1

2)Լուծե՛ք ռացիոնալ հավասարումը.

x=3 x=-7

x=4

x=-1

x=-2

x=-1

իմաստ չունի

3)Լուծե՛ք ռացիոնալ հավասարումը.

լուծում չունի

լուծում չունի

լուծում չունի

4)c-ն փոխարինե՛ք այնպիսի թվով, որ հավասարումն ունենա մեկ լուծում․

c=1 c=3

c=-4 c=13

c=2,5 c=1

c=15 c=25

1)Լուծե՛ք վերածվող հավասարումը.

ա) (x + 5)(x — 7) = 0

x∈{-5;7}

բ) 4x² = 0

x∈{0}

գ) 2(x — 5)² = 0

x∈{5}

դ) (3x + 12)(4 — x) = 0

x∈{-4;4}

ե) — 2x²(x + 1) = 0

x∈{-1;0}

զ) (5 — x)(x — 9) = 0

x∈{5;9}

2)Լուծեք հավասարումը․

ա)(x² + 5x + 6)(x + 2) = 0

x∈{-3;-2}

բ)(x² — 9x + 14)(x — 7) = 0

x∈{2;7}

գ)(x² + 7x + 10)(x² — 25) = 0

x∈{-2;-5}

դ)(x² — 7x + 12)(x² — 6x + 10) = 0

x∈{3;4}

ե)(x² — 15x — 16)(x² + 8x + 7) = 0

x∈{-7;-1;16}

զ)(x² — 4x + 3)(x² + 4x + 3) = 0

x∈{-3;-1;1;3;}

1)Հաշվե՛ք P(x) և Q(x) բազմանդամների քանորդն ու արդյունքը գրե՛ք ռացիոնալ արտահայտությամբ.

x2-3x-10+1/x+2

3x-4+1/2x+6

x2-120/x+11=x-11+1/x+11

x2-180/x-13+1/x+13

6×3+x2-42x+10/-x2+7=-6x-1*17/-x2+7

2×4-x3+11x-6/x3+5=2x-1+x-11/x3+5

2)Կատարեք մնացորդով բաժանում.
ա) x³ — 4x² + x + 6 -ը x + 1-ի, x − 2-ի, x — 3-ի վրա
բ) x⁴ + 2x³ + x² + 6 -ը x² + x + 1-ի, x + 2-ի վրա

1)Լուծեք անհավասարումները․

(-;1)U(2;+)

(2;4)

(-3;5)

(-;-8)U(7;+)

2)Լուծեք անհավասարումները․

(2;6)

(-;4)U(9;+)

(0.5;2)

(-;-2)U(1/3;+)

3)Լուծեք անհավասարումները․

(-2;1)U(3;+)

(-;-3)U(-1;2)

(-8;-1)U(5;7)U(7;+)

(-1;1)U(4;6)

4)Լուծեք անհավասարումները․

(-1;0)U (1/4;+)

(0;2)U(3;+)

(4;6,5)

(-;0)U(0;3)U(4;+)

5)Լուծեք անհավասարումները․

(-;-3)U(-1;2)U(3;+)

(-;-4)U(-1;4)U(6;+)

(-;-2)U(2;6)

(-1/5;1/5)U(1/5;5)