1)Հաշվել արտահայտության արժեքը․

11/7

29/39

1/20

1/9

2)Հաշվել արտահայտության արժեքը․

ա)|5a + 2| — |a — 2|=20, եթե a = 4

բ)|3a — 6| — |2a — 1|=-7, եթե a = -2

գ)|2a — 5| — |5a — 3|=-16, եթե a = -6

դ)|4a + 2| — |a|=4, եթե a = -2

3)Հաշվել արտահայտության արժեքը․

8

25

5

25

4)Լուծել խնդիրները․

1)8 տրակտոր 10 օրում վարում են 320 հա տարածք։

ա)3 տրակտորները 5 օրում քանի՞ հա տարածք կվարեն։

60

բ)8 տրակտորները քանի՞ օրում կվարեն 160 հա տարածք։

5

2)4 տրակտոր 7 օրում վարում են 280 հա տարածք։

ա)3 տրակտորները 4 օրում քանի՞ հա տարածք կվարեն։

120

բ)5 տրակտորները քանի՞ օրում կվարեն 300 հա տարածք։

6

3)5 տրակտոր 7 օրում վարում են 210 հա տարածք։

ա)2 տրակտորները 3 օրում քանի՞ հա տարածք կվարեն։

36

բ)4 տրակտորները քանի՞ օրում կվարեն 120 հա տարածք։

5

1)Տրված է y = x2 ֆունկցիայի գրաֆիկը: Այն y-ների առանցքի երկայնքով ձգեցին a անգամ, այնուհետև տեղաշարժեցին b միավորով ձախ և c միավորով ներքև։ Արդյունքում ստացվեց y = 5 * (x + 4)2 — 2 ֆունկցիայի գրաֆիկը: Գտե՛ք a-ն, b-ն ու c-ն:

a=5 b=4 c=2

2)Տրված է y = — x2 ֆունկցիայի գրաֆիկը: Այն y-ների առանցքի երկայնքով ձգեցին 3 անգամ, այնուհետև 5 միավորով աջ և 7 միավորով վերև։ Ո՞ր ֆունկցիայի գրաֆիկը ստացվեց:

y=3*(x-5)+7

3)Տրված է y = x2 ֆունկցիայի գրաֆիկը։ Այն սեղմեցին a անգամ, այնուհետև տեղաշարժեցին 4 միավորով ներքև։ Արդյունքում ստացվեց y = 1/8 * x2 — 4 ֆունկցիայի գրաֆիկը: Գտե՛ք a-ն:

8

4)Պատկերե՛ք ֆունկցիայի գրաֆիկը.

ա) y = (x + 1)2 + 3

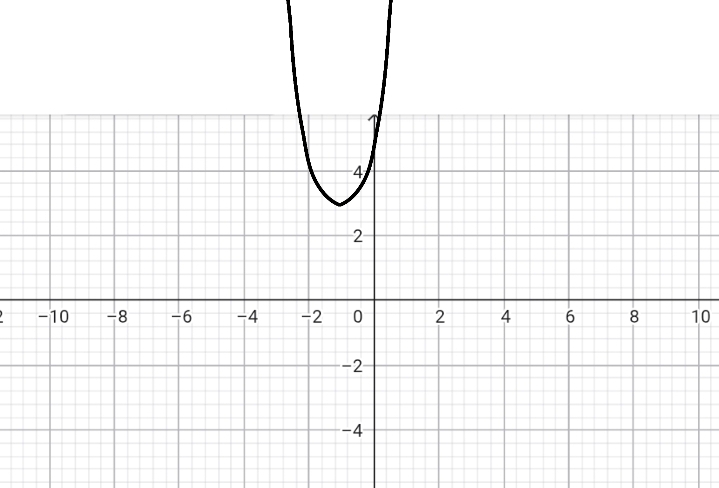
բ) y = 3 * (x — 2)2 — 1 ,

գ) y = — 2 * (x + 7)2 + 1

5)Գտե՛ք հետևյալ պարաբոլի գագաթի կոորդինատները.

ա) y = 2(x — 4)2

4;0

բ) y = — (x + 2)2 — 5

-2;-5

գ) y = x2 + 5

0;5

դ) y = 8 * (x — 11)2 + 20

11;20

ե) y = — 5/9 * (x + 3)2 + 1

-3;1

զ) y = 4 * (x — 3)2 — 12

3;-12

1)Տրված է y = x² ֆունկցիայի գրաֆիկը: Այն y-ների առանցքի երկայնքով ձգեցին a անգամ, այնուհետև տեղաշարժեցին b միավորով ձախ և c միավորով ներքև։ Արդյունքում ստացվեց y = 5 * (x + 4)² — 2 ֆունկցիայի գրաֆիկը: Գտե՛ք a-ն, b-ն ու c-ն:
a=5, b=4, c=2 

2)Տրված է y = — x² ֆունկցիայի գրաֆիկը: Այն y-ների առանցքի երկայնքով ձգեցին 3 անգամ, այնուհետև 5 միավորով աջ և 7 միավորով վերև։ Ո՞ր ֆունկցիայի գրաֆիկը ստացվեց:
y = 3 * (x-5) + 7

3)Տրված է y = x² ֆունկցիայի գրաֆիկը։ Այն սեղմեցին a անգամ, այնուհետև տեղաշարժեցին 4 միավորով ներքև։ Արդյունքում ստացվեց y = 1/8 * x² — 4 ֆունկցիայի գրաֆիկը: Գտե՛ք a-ն:
a=8

4)Պատկերե՛ք ֆունկցիայի գրաֆիկը.
ա) y = (x + 1)² + 3

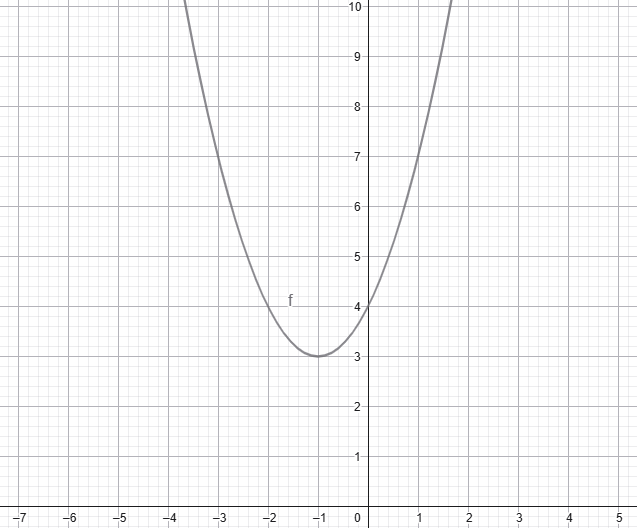
բ) y = 3 * (x — 2)² — 1

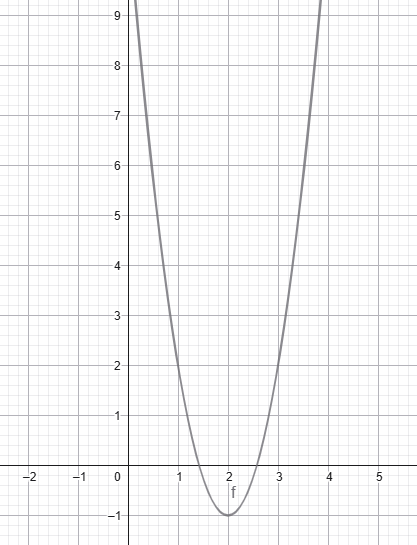
գ) y = — 2 * (x + 7)² + 1

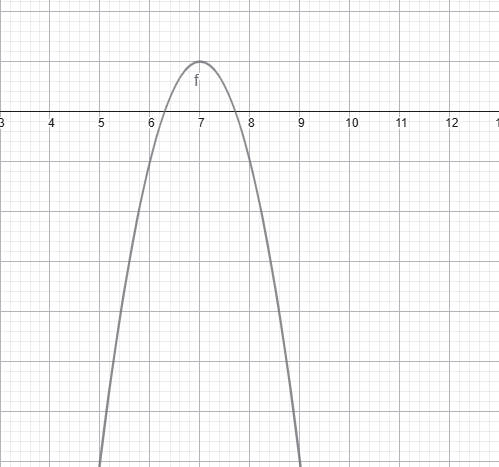
5)Գտե՛ք հետևյալ պարաբոլի գագաթի կոորդինատները.
ա) y = 2(x — 4)²
(4;0)
բ) y = — (x + 2)² — 5
(-2;-5)
գ) y = x² + 5
(0;5)
դ) y = 8 * (x — 11)² + 20
(11;20)
ե) y = — 5/9 * (x + 3)² + 1
(-3;1)
զ) y = 4 * (x — 3)² — 12
(3;-12)

6)Պարզե՛ք պարաբոլի ճյուղերի ուղղությունը: Դրանք հատվո՞ւմ են աբսցիսների առանցքի հետ.
ա) y = (x — 1)² + 3
Դեպի վեր, չի հատվում
բ) y = — 2 * (x — 5)² + 6
Դեպի ներքև, հատվում է
գ) y = — 7 * (x — 8)² — 14
Դեպի ներքև, չի հատվում
դ) y = 4x² — 16

ե) y = — 3 * (x + 4)² — 15

1)Հաշվել արտահայտության արժեքը․

16/7

7/5

4

6

23/24

1/5

2)Հաշվել արտահայտության արժեքը․

|-7| + |2| — |-3-2| =4

|-2| + |2| — |1-5| =0

|4a-3| — |2a-2|=5 , եթե a = -2

|2a-4| + |a+3|=8 , եթե a = -1

3)Հաշվել արտահայտության արժեքը․

27

27

4

4

4)Լուծել խնդիրները․

ա)Բադերը և խոզերը միասին ունեն 17 գլուխ և 44 ոտք։

Որքա՞ն բադ կա։

12

Որքա՞ն խոզ կա։

5

բ)Բադերը և խոզերը միասին ունեն 22 գլուխ և 58 ոտք։

Որքա՞ն բադ կա։

15

Որքա՞ն խոզ կա։

7

գ)Բադերը և խոզերը միասին ունեն 22 գլուխ և 56 ոտք։

Որքա՞ն բադ կա։

16

Որքա՞ն խոզ կա։

6

1)

a{2;3}

b{-1/2;-2}

c{8;0}

d{1;-1}

e{0;-2}

f{-1;0}

2)

x=-3i+1/5j

-2i-3j

-i

3j

j

3)

x=5,y=-2

-3,7

-4, 0

0, 0

4)

a+b={5;7}

a+b={4;1}

a+b={1;1}

a+b={-1;0}

5)

a-b={3;2}

a-b={6;0}

a-b={-1;9}

a-b={-7;-2}

6)

{6;4}

{9;6}

{-3;-2}

{-9;-6}

7)

a{-2;-4}

b{2;0}

c{0;0}

d{2;3}

e{-2;3}

1)y=f(x−166) ֆունկցիայի գրաֆիկը կառուցելու համար պետք է y=f(x) ֆունկցիայի գրաֆիկը տեղաշարժել 166 միավորով դեպի՝

• վերև
• ձախ
• աջ
• ներքև

2)Ո՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե y = 6x¹⁷ ֆունկցիայի գրաֆիկը Ox առանցքի ուղղությամբ տեղաշարժել 16 միավորով դեպի ձախ:

y=6(x+16)^17

3)y=1/2(x−198)¹³ + 62 ֆունկցիայի գրաֆիկը կառուցելու համար պետք է y = 1/2x¹³ ֆունկցիայի  գրաֆիկը տեղաշարժել 198 միավորով

• x-երի առանցքի ուղղությամբ դեպի ձախ
• x-երի առանցքի ուղղությամբ դեպի աջ
• y-երի առանցքի ուղղությամբ դեպի վերև
• y-երի առանցքի ուղղությամբ դեպի ներքև

և  62 միավորով

ա)x-երի առանցքի ուղղությամբ դեպի աջ

բ)y-երի առանցքի ուղղությամբ դեպի ներքև

գ)x-երի առանցքի ուղղությամբ դեպի ձախ

դ)y-երի առանցքի ուղղությամբ դեպի վերև

4)Ո՞ր ֆունկցիայի գրաֆիկը կստացվի, եթե  y=10x³ ֆունկցիայի գրաֆիկը Oy առանցքի ուղղությամբ 8 միավորով տեղաշարժվի դեպի վերև:

y=10(x)^3+8

5)Նկարում պատկերված է f(x) ֆունկցիայի գրաֆիկը։ Գծե՛ք f(x — a) ֆունկցիայի գրաֆիկը.
ա)a = 3
բ)a = 2
գ)a = — 1
դ)a = 3
ե)a = — 2
զ)a = 4
է)a = -3
ը)a = -2

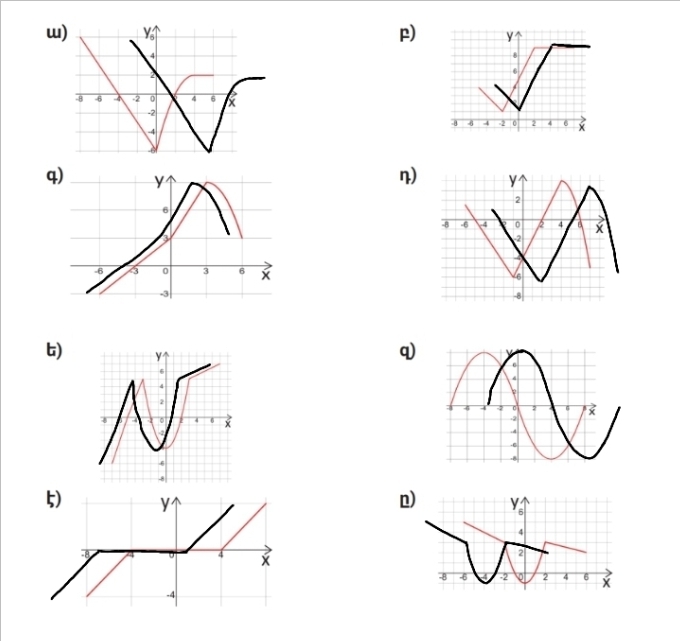
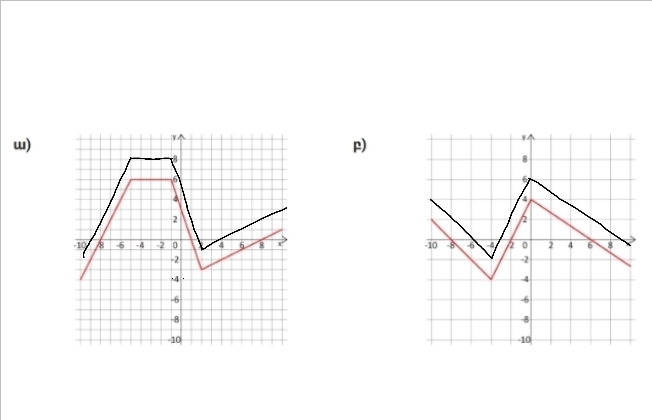
6)Նկարում պատկերված է f(x — 2) ֆունկցիայի գրաֆիկը: Գծե՛ք f(x) ֆունկցիայի գրաֆիկը.

7)Գտնել A ∩ B բազմությունը, եթե A = {0; 3; 4; 6}, B = {3; 6; 9}։

{3;6}

8)Գտնել A ∩ B բազմությունը, եթե A = {1; 3; 6; 9}, B = {5; 6; 8}։

{6}

9)Գտնել A U B բազմությունը, եթե A = {0; 1; 2; 4}, B = {1; 2; 5}։

{0;1;2;4;5}

10)Գտնել A U B բազմությունը, եթե A = {0; 3; 6; 9}, B = {0; 3; 8}։

{0;3;6;8;9}

11)Գտնել A U B բազմությունը, եթե A = {7}, B = {4; 6}։

{4;6;7}

1)Գծե՛ք ֆունկցիայի գրաֆիկ, որն ունի հետևյալ նշանապահպանման միջակայքերը․
ա) (- ∞, 1) -ում՝ դրական, (1, 2)-ում՝ բացասական, (2, ∞) -ում՝ դրական,
բ) (- ∞, — 2) -ում՝ դրական, (−2, 0)-ում՝ դրական, (0, 5)-ում՝ բացասական, (5, +∞) -ում՝ դրական,
գ) (- ∞, -√8)-ում՝ բացասական, (- √8, √7) -ում՝ դրական, (√7, +∞) -ում՝ բացասական:

ա. Գրաֆիկ՝ նշանապահպանման միջակայքներով՝ (- ∞, 1), (1, 2), (2, ∞)

Այս հարցում պետք է ունենալ մի ֆունկցիա, որի նշանապահպանման միջակայքները հետևյալն են՝

• (- ∞, 1) — դրական
• (1, 2) — բացասական
• (2, ∞) — դրական

Այսպիսի նշանափոխություն ունեցող ֆունկցիան կարող է լինել օրինակ f(x)=(x−1)(x−2)f(x)=(x−1)(x−2). Սա բացատրում է նշանափոխությունների և ինտերվալների ամենաբավարար լուծումը:

բ. Գրաֆիկ՝ նշանապահպանման միջակայքներով՝ (- ∞, -2), (-2, 0), (0, 5), (5, +∞)

Այս դեպքում ֆունկցիան պետք է ունենա հետևյալ նշանափոխությունները՝

• (- ∞, -2) — դրական
• (-2, 0) — դրական
• (0, 5) — բացասական
• (5, +∞) — դրական

Օրինակ, կարող է լինել f(x)=(x+2)(x)(x−5)f(x)=(x+2)(x)(x−5), որը այս նշանափոխությունները կապում է միջակայքների հետ:

գ. Գրաֆիկ՝ նշանապահպանման միջակայքներով՝ (- ∞, -√8), (-√8, √7), (√7, ∞)

Հակառակի նշանափոխությունները հետևյալն են՝

• (- ∞, -√8) — բացասական
• (-√8, √7) — դրական
• (√7, ∞) — բացասական

Ֆունկցիան կարող է լինել f(x)=(x2+8)(x2−7)f(x)=(x2+8)(x2−7).

2)Ո՞ր գրաֆիկով ֆունկցիայի նշանապահպանման միջակայքերն են.
ա) (- ∞, — 3) (0, 4)-ում՝ դրական, (–3, 0), (4, +0)-ում՝ բացասական,
բ) (- ∞, — 1) , (-1, 2)-ում՝ բացասական, (2, +0)-ում՝ դրական,
գ) (- ∞, — 2) (-1, 1)-ում՝ բացասական, (−2, −1), (1, +0)-ում՝ դրական:

ա. (- ∞, — 3) (0, 4)-ում՝ դրական, (–3, 0), (4, ∞)-ում՝ բացասական

Մասնավորապես, այս գրանցումը ամենայն հավանականությամբ ցույց է տալիս որոշակի ֆունկցիա, որտեղ նշանափոխությունները կհամապատասխանեն այս միջակայքներին:

բ. (- ∞, — 1) , (-1, 2)-ում՝ բացասական, (2, +∞)-ում՝ դրական

Այս գրաֆիկում նույնպես պետք է փնտրել այնպիսի ֆունկցիա, որն ունի նշանափոխություններ այս միջակայքներում:

գ. (- ∞, — 2) (-1, 1)-ում՝ բացասական, (−2, −1), (1, ∞)-ում՝ դրական

Այս վերը նշված գրաֆիկին պետք է ունենալ ծավալվող հատվածներ նշանափոխությունների փոխարինման համար:

3)Գծե՛ք ֆունկցիայի գրաֆիկ, որը բավարարում է հետևյալ երկու պայմաններին․
1) անցնում է կոորդինատային հարթության (2, 3) կետով,
2) (–∞, 0)-ում դրական է, (0, 1)-ում՝ բացասական, (1, +∞)-ում՝ դրական:

1. Անհրաժեշտ է, որ ֆունկցիան անցնի կոորդինատային հարթության (2, 3) կետով։
2. Ունի նշանափոխությունները՝

• (–∞, 0) — դրական,
• (0, 1) — բացասական,
• (1, +∞) — դրական:

Ֆունկցիան կարող է լինել, օրինակ, f(x)=x(x−1)(x−2)+3f(x)=x(x−1)(x−2)+3:

4)Գծե՛ք ֆունկցիայի գրաֆիկ, որը բավարարում է հետևյալ երկու պայմաններին.
1) անցնում է կոորդինատային հարթության (−2, 1), (0, −1) և (3, −1) կետերով, 
2) նշանապահպանման միջակայքերն են՝ (-∞, -1), (-1, 1) և (1, +∞):

1. Անհրաժեշտ է, որ ֆունկցիան անցնի կոորդինատային հարթության (−2, 1), (0, −1) և (3, −1) կետերով:
2. Ֆունկցիան պետք է ունենա նշանապահպանման միջակայքներ՝ (-∞, -1), (-1, 1) և (1, +∞):

Այսպիսի ֆունկցիայի հնարավոր տարբերակը կարող է լինել f(x)=(x+2)(x−3)(x+1)f(x)=(x+1)(x+2)(x−3):

5)Գծե՛ք ֆունկցիայի գրաֆիկ, որը բավարարում է հետևյալ երկու պայմաններին․
1) նշանապահպանման միջակայքերն են՝ (-∞, — 2) ,(-2, 1) և (1, +∞) ,
2) անցնում է կոորդինատային հարթության (–5, 1), (-1, -2), (2, −2) կետերով։

1. Միջակայքներն են՝ (-∞, — 2), (-2, 1) և (1, +∞):
2. Անհրաժեշտ է, որ ֆունկցիան անցնի կոորդինատային հարթության (–5, 1), (-1, -2), (2, −2) կետերով։

Այս խնդիրը լուծելու համար առաջարկում եմ ֆունկցիա՝ f(x)=(x+2)(x−1)f(x)=(x+2)(x−1):

6)Գտնել բաժանելին, եթե բաժանարարը 9 է, քանորդը՝ 7, իսկ մնացորդը՝ 5:

Բաժանելին գտնելու համար կարող ենք կիրառել բաժանման բանաձևը՝բաժանելին=բաժանարար×քանակ+մնացորդբաժանելին=բաժանարար×քանակ+մնացորդբաժանելին=9×7+5=63+5=68բաժանելին=9×7+5=63+5=68

Ավտոմատապես բաժանելին 68 է:

7)Գտնել բաժանելին, եթե բաժանարարը 7 է, քանորդը՝ 5, իսկ մնացորդը՝ 3:

38բաժանելին=7×5+3=35+3=38

Բաժանելին 38 է:

8. Գտնել բաժանելին՝ բաժանարարը 9 է, քանորդը՝ 8, իսկ մնացորդը՝ 6

բաժանելին=9×8+6=72+6=78բաժանելին=9×8+6=72+6=78

Բաժանելին 78 է:

9)Գտնել բաժանելին, եթե բաժանարարը 6 է, քանորդը՝ 4, իսկ մնացորդը՝ 1:

բաժանելին=6×4+1=24+1=25

Բաժանելին

Առաջադրանքներ․

1)Գտե՛ք պատկերված գրաֆիկով ֆունկցիայի նշանապահպանման միջակայքերը․

ա(-;-1) +

(-1;3) –

(3;+) +

բ (-;-2) –

(-2;1)+

(1;+) +

գ (-;-2) +

(-2;0) +

(0;3) –

(3;+) +

դ (-;-2) –

(-2;2) +

(2;3) –

(3;+) +

ե (-;-3) +

(-3;2) –

(2;+) +

զ (-;-2) –

(-2; 0,5) +

(0,5;+) +

2)Գծե՛ք ֆունկցիայի գրաֆիկ, որի նշանապահպանման միջակայքերը կլինեն․

ա) (−∞, −2), (−2, 1), (1, +∞),

բ) (−∞; −  4/5), (−  4/5; 0), (0; 3), (3; +∞),

գ) (−∞; 3), (3; +∞),

դ) (−∞, +∞):

3)Գծե՛ք ֆունկցիայի գրաֆիկ, որի նշանապահպանման միջակայքերի գծապատկերը կունենա հետևյալ տեսքը․

4)Ճարտարապետ Ռաֆայելը տարվա ընթացքում նախագծեց 25 առանձնատուն՝ 10 փոքր ու 15 մեծ։Փոքր առանձնատներից յուրաքանչյուրի համար նա վաստակում է 240 000 դրամ, իսկ մեծի համար՝ 450 000։
ա) Մեկ պատվերից միջինում որքա՞ն գումար է աշխատում Ռաֆայելը։

2400000+6750000=9150000

9150000:2=4575000
բ) Շինարարության ընթացքում Ռաֆայելը փոքր առանձնատուն այցելում է 7 անգամ, իսկ մեծ առանձնատուն՝ 12։ Յուրաքանչյուր այցելության ժամանակ նա ծախսում է միջինում 1500 դրամի մեքենայի վառելիք։ Տարվա ընթացքում որքա՞ն շահույթ ստացավ Ռաֆայելը։

1500*7=10500

1500*12=18000

18000+10500=28500

9150000-28500=9121500

5)Գտնել (-5; 36) միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

36-(-5)-1=40

6)Գտնել (34; 78) միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

78-34-1=34

7)Գտնել (23; 57] միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

57-23=34

8)Գտնել [-3; 45) միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

45-(-3)=48

9)Գտնել [23; 123] միջակայքին պատկանող բոլոր ամբողջ թվերի քանակը։

1)Oxy հարթության վրա շրջանագիծը տրված է հետևյալ հավասարումով.

ա) x² +y² =36,

բ) (x — 3)² + (y — 5)² = 25

Ինչի՞ են հավասար շրջանագծի կենտրոնի կոորդինատները և շառավիղը:

(0;0)

R=6

(3;5)

R=5

2)Շրջանագիծը տրված է (x + 4)² + (y — 3)² = 2, 56 հավասարումով: Նշե՛ք, թե (-4, 4), (-2, 1), (-2, 3), (-5, 4) կետերից որոնք են ընկած`

ա) շրջանագծի վրա,

բ) տրված շրջանագծով եզերված շրջանի ներսում,

(-4;4)

(-5;4)

գ) տրված շրջանագծով եզերված շրջանից դուրս:

(-2; 1)

(-2; 3)

3)Գրե՛ք r շառավիղով և O կենտրոնով շրջանագծի հավասարումը, եթե`

ա) r = 1 Օ(0, -7),

x²+(y+7)²=1

բ) r = 5 O(1, -2)

(x-1)²+(y+2)²=25

գ) r = 0,5 Օ(-3, -7)

(x+3)²+(y+7)²=0.25

4)Գրե՛ք այն շրջանագծի հավասարումը, որի կենտրոնը կոորդինատների սկզբնակետն է, և որն անցնում է՝

ա) (1, 2)

1+4=5

x²+y²=5

բ) (-3, 5),

9+25=34

x²+y²=34

գ) (4, -3) կետով

16+9=25

x²+y²=25

5)Գրե՛ք M կենտրոնով և N կետով անցնող շրջանագծի հավասարումը, եթե՝

ա) M(−1, 2), N(0, 5),

(0+1)²+9=r²

r²=10

(x+1)+(y-2)²=10

բ) M(0, 3), N(-2, 6):

1)Նշե՛ք x-ի որևէ արժեք, որի դեպքում արտահայտության արժեքը դրական է.

x=3

x=4

x=2

x=1

2)Նշե՛ք x-ի որևէ արժեք, որի դեպքում արտահայտության արժեքը բացասական է.

x=6

x=-1

x=-4

x=-5

3)Պարզե՛ք արտահայտության նշանը տրված կետում․

+

–

–

–

–

–

–

–

–

4)Գտե՛ք արտահայտության նշանը․

–

–

+

–

–

–

+

–