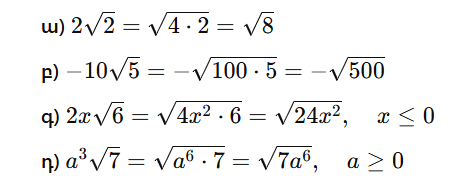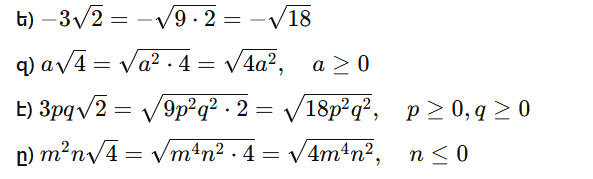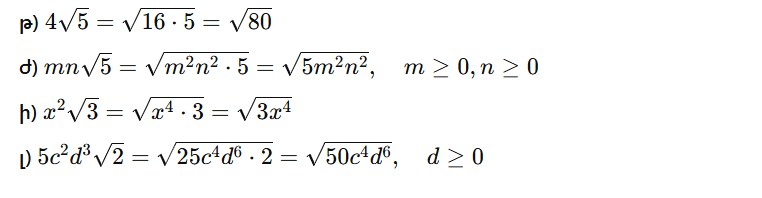1)Գտե՛ք արտահայտության նշանապահպանման միջակայքերն ու այդ միջակայքերում արտահայտության նշանը.

Ա (-;-5)-

(-5;2)+

(2;+) +

Բ (-;1)

(1;2.5)

(2.5;+)

Գ (-;√7) +

(√7;√8) +

(√8;+)+

Դ (-;-2) –

(-2;√2) +

(√2;+) +

Ե (-;1)+

(1;4) –

(4;+) +

զ (-;-14348907) +

(-14348907;1024) –

(1024;+) +

2)Գտե՛ք արտահայտության նշանապահպանման միջակայքերն ու այդ միջակայքերում արտահայտության նշանը․

աx=2

x=5

x=12

(-;2) –

(2;5) +

(5;12) –

(12;+) +

բ x=1

x=3125

(-;1) +

(1;3125) –

(3125;+) +

գ (-;-10) –

(-10;11) +

(11;100) –

դ(-;-1) –

(-1;2.8) +

(2.8;4) –

(4;+) +

ե (-;-5) –

(-5;-1) +

(-1;9) –

(9;+) +

զ (-;-32) –

(-32;1) +

(1;64) –

(64;+) +

է (-;-2.2) –

(-2.2;6) +

(6;12094627905536) –

(12094627905536;+)+

ը (-;-8) –

(-8;14348907) +

(14348907;244140625) –

(244140625;+) +

թ (-;2,8) –

(2,8;9) +

(9;21,9) –

(21,9;+) +

1)Գտե՛ք A և B ծայրակետերով հատվածի միջնակետի կոորդինատները, եթե

ա) A(2; 3), B(-2; 1)

0;2

բ) A(1; 8), B(5; 5)

3;6.5

2)Գտե՛ք AB հատվածի B ծայրակետի կոորդինատները, եթե C(2; — 1) կետը այդ հատվածի միջնակետն է, իսկ A ծայրակետը ունի (3; 5) կոորդինատները:

1;-7

3)Գտե՛ք B կետի կոորդինատները, եթե այն A(3; −4) կետի համաչափն է կոորդինատների սկզբնակետի նկատմամբ:

-3;4
4)Գտե՛ք A(-2; 3) կետի` x-երի առանցքի նկատմամբ համաչափ B
կետի կոորդինատները:

-2;-3

5)Գտե՛ք C(7; 2) կետի՝ y-ների առանցքի նկատմամբ համաչափ D
կետի կոորդինատները:

-7;2

6)Ինչի՞ է հավասար A(2; — 3) կետի հեռավորությունը՝

ա) x-երի առանցքից

2;3

բ) y-ների առանցքից

-2;3

գ) կոորդինատների սկզբնակետից
7)Գտե՛ք A և B կետերի հեռավորությունը, եթե.

ա) A(1;-3), B(1; 2)

dKL=√(1-1)²+√(2+3)²=√5²=√25=5

բ) A(2; 3), B(1; −1)

dKL=√(1-2)²+√((-1-3)²=√(1+16)²=√289=17

գ) A(0; 2), B(4; -1)

dKL=√(4-0)²+√(-1-2)²=√(8-9)²=1

8)Գտեք ABC եռանկյան պարագիծը, եթե A(8; 1), B(5; -3), C(11; -3)։

AB=√(5-8)²+√(-3-1)²=√(-3-4)²=√49=7

BC=√(11-5)²+√(-3-5)²=√(6+8)²=√4=2

CA=√(11-8)²+√(-3-1)²=√(6+16)²=√484=22

P=7+2+22=31

9)Գտեք Ox առանցքի այն կետի կոորդինատները, որը գտնվում է A(5;3) կետից 5 հեռավորության վրա:

5;-3

1)Հաշվեք քառակուսային եռանդամի տարբերիչը.

ա)2x² + 5x — 3

D=b²-4ac=25+24=49

բ)x² + 6x + 9

D=36-36=0

գ)x² + 2x + 2

D=4-8=-4

դ)2x² — 5x — 7

D=25+56=81

ե)6x² + x — 2

D=1+48=49

զ)3x² + 4x + 5

D=16-60=-44

2)Լուծե՛ք քառակուսային հավասարումը.

ա)2y² — 9y + 10 = 0

D=81-80=1

x1=(-b+√D)/2a=9+1/4=2.5

x2=(-b-√D)/2a=9-1/4=2

բ)16a² — 40a + 25 = 0

D=1600-1600=0

x=40/32

գ)x² — 8x + 16 = 0

D=64-64=0

x=8-1=7

դ)9z² — 30z + 25 = 0

D=900-900=0

x=30-18=12

ե)7x² — 13x — 20 = 0

D=169+560=729

x1=(-b+√D)/2a=13+27/14=40/14

x2=(-b-√D)/2a=13-27/14=-1

1)Հաշվե՛ք հավասարման տարբերիչն ու որոշե՛ք հավասարման արմատների քանակը.

ա) x² — 3x + 1 = 0

b-4ac=9-4=5

2 արմատ

բ) x² — 4x + 4 = 0

16-16=0

1 արմատ
գ) 2x² + 3x + 1 = 0

9-8=1

2 արմատ
դ) 3x² + 5 = 0

0-60=-60

լուծում չունի
ե) 2x² — x + 1 = 0

1-8=-7

լուծում չունի

2)Լուծե՛ք քառակուսային հավասարումը.

ա) 3y² — 5y — 2 = 0

25+24=49

x1=5+7/6=2

x2=5-7/6=-1/3

բ) 9z² — 30z + 25 = 0

900-900=0

x=30+√0/18=5/3
գ) x² — 8x + 16 = 0

64-64=0

x=8+√0/1=8
դ) y² — 11y — 152 = 0

121+608=729

x1=11+√729/1=38

x2=11-√729/1=-16

ե) — 7x² + 5x = 0

d=25

x=-5+√25/-14=0
զ) 7x² — 13x — 20 = 0

169+560=729

D=5

2 արմատ

բ) x² — 4x + 4 = 0

D=16-16=0 

1 արմատ
գ) 2x² + 3x + 1 = 0

D=9-8=1

D>0

2 արմատ
դ) 3x² + 5 = 0

D=0-60=-60

Լուծում չունի
ե) 2x² — x + 1 = 0

D=1-8=-7

D<0

Լուծում չունի

2)Լուծե՛ք քառակուսային հավասարումը.

ա) 3y² — 5y — 2 = 0

D=25-24=1o

y1=-b+√D/2a=5+1/6=1
բ) 9z² — 30z + 25 = 0

D=900-900=0

y2=-b-√D/2a=5-1/6=4/6=2/3
գ) x² — 8x + 16 = 0

D=64-64=0

z1=z2
դ) y² — 11y — 152 = 0

D=121-608=-485

Լուծում չունի
ե) — 7x² + 5x = 0

D=25-0=25

X1=-b+√D/2a=-5+5/-14=0

X2=-b-√D/2a=-5-5/-14=-10/14

զ) 7x² — 13x — 20 = 0

D=169-560=-391

Լուծում չունի

3)Լուծե՛ք քառակուսային հավասարումը.

ա) 3x² — 7x + 4 = 0

49-48=1

X1=7+1/6=8/6=4/3

X2=7-1/6=1

բ) 5y² — 6y + 1 = 0

D=36-20=16

X1=6-4/10=2/10=1/5

X2=6+4/10=1
գ) x² — 10x + 25 = 0

D=100-100=0

X1=X2
դ) 2y² — 9y + 10 = 0

D=81-80=1

X1=9+1/4=10/4=5/2

X2=9-1/4=2
ե) 5a² + 26a — 24 = 0

D=676+480=1156

X1=-26+34/10=8/10=4/5

X2=-26-34/10=50/10=-5/1=-5

1)Հաշվե՛ք հավասարման տարբերիչն ու որոշե՛ք հավասարման արմատների քանակը.

ա) x² — 3x + 1 = 0 

D=5

2 արմատ

բ) x² — 4x + 4 = 0

D=16-16=0 

1 արմատ
գ) 2x² + 3x + 1 = 0

D=9-8=1

D>0

2 արմատ
դ) 3x² + 5 = 0

D=0-60=-60

Լուծում չունի
ե) 2x² — x + 1 = 0

D=1-8=-7

D<0

Լուծում չունի

2)Լուծե՛ք քառակուսային հավասարումը.

ա) 3y² — 5y — 2 = 0

D=25-24=1o

y1=-b+√D/2a=5+1/6=1
բ) 9z² — 30z + 25 = 0

D=900-900=0

y2=-b-√D/2a=5-1/6=4/6=2/3
գ) x² — 8x + 16 = 0

D=64-64=0

z1=z2
դ) y² — 11y — 152 = 0

D=121-608=-485

Լուծում չունի
ե) — 7x² + 5x = 0

D=25-0=25

X1=-b+√D/2a=-5+5/-14=0

X2=-b-√D/2a=-5-5/-14=-10/14

զ) 7x² — 13x — 20 = 0

D=169-560=-391

Լուծում չունի

3)Լուծե՛ք քառակուսային հավասարումը.

ա) 3x² — 7x + 4 = 0

49-48=1

X1=7+1/6=8/6=4/3

X2=7-1/6=1

բ) 5y² — 6y + 1 = 0

D=36-20=16

X1=6-4/10=2/10=1/5

X2=6+4/10=1
գ) x² — 10x + 25 = 0

D=100-100=0

X1=X2
դ) 2y² — 9y + 10 = 0

D=81-80=1

X1=9+1/4=10/4=5/2

X2=9-1/4=2
ե) 5a² + 26a — 24 = 0

D=676+480=1156

X1=-26+34/10=8/10=4/5

X2=-26-34/10=50/10=-5/1=-5

1)Անվանեք քառակուսային եռանդամի a, b և c գործակիցները`

ա) 3x² + 4x + 5
→ a = 3, b = 4, c = 5

բ) 6x² + x – 2
→ a = 6, b = 1, c = –2

գ) 2x² – 5x – 7
→ a = 2, b = –5, c = –7

դ) x² – x + 7
→ a = 1, b = –1, c = 7

ե) –5x² + 3x – 1
→ a = –5, b = 3, c = –1

զ) –x² + x + 1
→ a = –1, b = 1, c = 1

2)Կազմեք քառակուսային եռանդամ տրված գործակիցներով`

ա) a = 3; b = 4; c = 5
→ 3x² + 4x + 5

բ) a = 1; b = –1; c = 2
→ x² – x + 2

գ) a = 3; b = –2; c = 6
→ 3x² – 2x + 6

դ) a = –1; b = 3; c = –2
→ –x² + 3x – 2

3)Հաշվեք քառակուսային եռանդամի տարբերիչը`

ա) 2x² + 5x + 3
a = 2, b = 5, c = 3
D = 5² – 4·2·3 = 25 – 24 = 1

բ) 2x² – 5x + 3
a = 2, b = –5, c = 3
D = (–5)² – 4·2·3 = 25 – 24 = 1

գ) 2x² + 5x – 3
a = 2, b = 5, c = –3
D = 5² – 4·2·(–3) = 25 + 24 = 49

դ) x² + 2x + 1
a = 1, b = 2, c = 1
D = 2² – 4·1·1 = 4 – 4 = 0

ե) x² – 4x + 5
a = 1, b = –4, c = 5
D = (–4)² – 4·1·5 = 16 – 20 = –4

զ) –3x² + 5x – 2
a = –3, b = 5, c = –2
D = 5² – 4·(–3)·(–2) = 25 – 24 = 1

է) 2x² + 5x – 3
(Նույնն է, ինչ գ) ) → D = 49

ը) x² + 6x + 9
a = 1, b = 6, c = 9
D = 6² – 4·1·9 = 36 – 36 = 0

թ) x² + 2x + 2
a = 1, b = 2, c = 2
D = 2² – 4·1·2 = 4 – 8 = –4

1)Պարզե՛ք, բազմանդամը քառակուսային եռանդա՞մ է, թե՞ ոչ. D=b²-4ac

ш) 3x² — 7x + 3 այո

ա) x² + y ոչ

բ) (1 — x)(2x + 1) այո

գ) 4x³ — 7x² + x ոչ

դ) 3x ոչ

ե) (y + x)(y — x) — y² ոչ

զ) — 1.1x + 3.9(4) ոչ

է) — 3y² — 7 ոչ

ը) (xy — 1)²+ 5 ոչ

թ) 2xx + 3x — x + 25 այո

ժ) (x²)² + 3x + 7 ոչ

ժա) (1 — x) * x + (2x + 1)² այո

2)Անվանե՛ք քառակուսային եռանդամի գործակիցները.

ա) x²+ 5x + 7 a=1, b=5, c=7

բ) — 3x² + 1 a=-3, b=0, c=1

գ) 2x² — 3x + 5

A=2, b=-3, c=5

դ) 9x² — 15

A=9, b=0, c=-15

ե) 2x(3x — 1) + 3x — 4

A=6, b=1, c=-4

զ) (- x²)/4 + 2

A=-1/4, b=0, c=2

է) — x² — 14x + 3

A=-1, b=-14, c=3

ը) — x² + 7x

A=-1,b=7, c=0

թ)6x² — 13

A=6, b=0, c=-13

ժ) — 4x² + x — 6

A=-4, b=1, c=-6

3)Կազմե՛ք ax² + bx + c քառակուսային եռանդամը, երբ.

ա) a = 2, b = 7, c = 1

2x²+7x+1

բ) a = 1, b = — 2, c = — 2

X²-2x-2

գ) a = — 1, b = 2, c = 3

-x²+2x+3

դ) a = — 1/2, b = 3, c = 3/4

-1/2x²+3x-3/4

ե) a = — 3, b = 0, c = — 5

-3x²-5

զ) a = 4, b = 0, c = — 3

4x²-3

է) a = 2, b = — 5, c = 0

2x²-5x

ը) a = — 7, b = 2, c = 0

-7x²+2x

թ) a = — 1, b = 0, c = 0

-x²

1)Հաշվե՛ք․

ա) √8 · √8 = √(8×8) = √64 = 8

բ) √98 · √50 = √(98×50) = √4900 = 70

գ) √640 · √1000 = √(640×1000) = √640000 = 800

դ) √3 · √75 = √(3×75) = √225 = 15

ե) √40 · √10 = √(40×10) = √400 = 20

զ) √25000 · √1000 = √(25000×1000) = √25000000 = 5000

է) √20 · √45 = √(20×45) = √900 = 30

ը) √27000 · √30 = √(27000×30) = √810000 = 900

2)Արտադրիչը տարեք արմատանշանի տակ`

3)Արտադրիչը դուրս բերեք արմատանշանի տակից`

շ) √(2/9) = √2 / 3

պ) √(3/16) = √3 / 4

ք) √(40/81) = √40 / 9 = 2√10 / 9

ն) √(72/25) = √72 / 5 = 6√2 / 5

տյ) √(12 * 1/2) = √6

քյ) √(1 * 1/4) = √1/2 = 1 / √2 = √2 / 2 (ռացիոնալացված տարբերակով)

տ) √(x³ / 9) = x√x / 3

թ) √(7a / 16b²) = √7 * √a / (4b) = √7a / 4b

պ) √(3m³n² / 4a²b) = (mn√(3m)) / (2a√b)

դ) √(25x²y³ / mn⁷) = (5xy√y) / (√m * n³√n)

հ) √((0.1x) / 10y²) = √(x / 100y²) = √x / (10y)

վ) √(5m³ / 0.5n) = √(10m³ / n) = m√(10m) / √n

4)Հաշվե՛ք․

1)Արդյո՞ք նշված արտահայտությունն իմաստ ունի.

ա այո

բ այո

գ ոչ

դ այո

ե ոչ

զ այո

է այո

ը այո

թ ոչ

ժ ոչ

2)Գտե՛ք տրված կողմի երկարությամբ քառակուսու մակերեսը: Հարմարության համար կարելի է փոխել չափման միավորը.

ա) 3 մ

9մ

բ) 9 կմ

81կմ

գ) 0.05 կմ

2500մ

դ) 2.8 սմ

784մմ

ե) 200 սմ

4մ

զ) 6000 մմ

36մ

է) 80 դմ

64մ

ը) 0.9մ

8100սմ

թ) 1.3 սմ

169մմ

ժ) 0.000003 կմ

9մմ

3)Թիվը բարձրացրե՛ք քառակուսի.

1

49

1,44

0,01

5

1,222

14

0

17,64

-6,8

4)Գտե՛ք քառակուսու կողմի երկարությունը, եթե նրա մակերեսը հավասար է.

ա) 25 մ² =5մ

բ) 100 մմ² =10մմ

գ) 49 մ² =7մ

դ) 0.01 սմ² =0,1սմ

ե) 64 դմ² =8դմ

զ) 0.09 սմ² =0,9սմ

է) 2.56 մ² =1,6մ

ը) 10000 սմ² =100սմ

թ) 144 սմ² =12սմ

ժ) 1.69 կմ² =1,3կմ

5)Հաշվե՛ք արտահայտության արժեքը.

2

5

4

-1

0,1

10

100

21

-12

1000

Առաջադրանքներ․

1)Լուծե՛ք անհավասարումների համակարգը․

ա)

x∈(5;8)

բ)

լուծում չունի

գ)

x∈(5;6)

դ)

լուծում չունի

ե)

x=2

2)Լուծե՛ք անհավասարումների համակարգը․

ա)

x∈(0;10)

բ)

x∈(-5;-1)

3)Լուծե՛ք անհավասարումների համակարգը․

ա)

x∈(0;+∞)

բ)

x∈(-8;-∞)

գ)

x∈(01;2)

դ)

x∈(3;+∞)

ե)

x=3

4)Լուծե՛ք անհավասարումների համակարգը․

ա)

լուծում չունի

բ)

x∈(-7;4)