Խնդիր 1 Արթուրն ու Մերին մետաղադրամ են նետում: Եթե մետաղադրամն ընկնում է այնպես, որ երևում է դրամի արժեքը, հաղթողը Մերին է, և Արթուրը նրան պետք է տա 2 կոնֆետ: Եթե դրամն ընկնում է այնպես, որ երևում է զինանշանը, հաղթում է Արթուրը, և Մերին Արթուրին պետք է տա 3 կոնֆետ: 30 անգամ դրամը նետելուց հետո նրանցից յուրաքանչյուրն ուներ այնքան կոնֆետ, որքան խաղից առաջ: Քանի՞ անգամ էր հաղթել Արթուրը:
Արթուրը հաղթել է 12 անգամ։
Խնդիր 2
Քառանիշ թվի հարյուրավորների տեղում 3 թիվն է, մնացած երեք թվանշանների գումարը նույնպես 3 է: Քանի՞ այդպիսի թիվ կա:
6 այդպիսի քառանիշ թիվ կա։
Խնդիր 3
1-ից մինչև 9 թվերից ընտրված տասներկու թվեր պետք է գրել ուղղանկյան վանդակներում այնպես, որ յուրաքանչյուր տողում գրված թվերի գումարներն իրար հավասար լինեն, և յուրաքանչյուր սյունակում գրված թվերի գումարները նույնպես հավասար լինեն: Թվանշաններից մի քանիսն արդեն գրված են: Ի՞նչ թիվ պետք է գրված լինի մոխրագույն վանդակում:
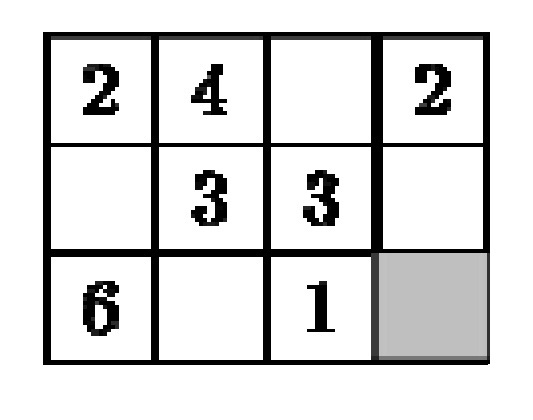
Մոխրագույն վանդակում պետք է լինի թիվը՝
6:Խնդիր 4
Եթե գումարենք յոթանիշ թվի թվանշանները, կստացվի 6: Ինչի՞ է հավասար այդ թվանշանների արտադրյալը:
Պատասխան՝ 0։
Խնդիր 5
Ոսկերիչն ունի 12 երկօղակ շղթա: Նա ցանկանում է դրանցից պատրաստել մի մեծ շղթա: Այդ անելու համար նա պետք է մի քանի օղակ բացի և հետո դրանք փակի: Ամենաքիչը քանի՞օղակ նա պետք է բացի:

Պատասխան՝ ամենաքիչը 11 օղակ պետք է բացել։







