16-20.12.2024

1.  Մայրենի լեզվի ֆլեշմոբի քննարկում։ 

2.  Ընթերցել ամսագրային նյութերը և նյութերի տակ գրել քոմենթ՝ 

Գրաշխարհ

Այս տեքստի տակ գրեցի մեկնաբանությունս ՝

Մենք բոլորս փոքր տարիքում երազում էինք Ձմեռ պապիկից նվեր ստանալ: Բայց որ սկսում ենք մեծանալ, մենք այլևս չենք հավատում, որ իրական Ձմեռ պապ գոյություն ունի: Ես միշտ մտածում էի, կարելի է արդյո՞ք հակառակն անել ու Ձմեռ պապիկին նվեր տալ:Եվ եթե չգտնեմ Ձմեռ պապիկ, ապա նվեր կտամ իմ իսկական ու բարի պապիկին: Այնպիսի նվեր, որը միշտ հիշվի: Ես կնվիրեմ իմ պապիկին առողջություն ու հանգստություն: Կուզեի, որ նա շատ երկար ապրեր և իր ներկայությամբ միշտ հարստացներ իր զավակների կյանքը: Սիրում եմ լսել նրա հետաքրքիր պատմությունները Հայաստանի և նրա մարդկանց մասին: Ես իմ պապիկին կնվիրեմ նաև իմ գեղեցիկ նկարները: Ես հաճախ նկարում եմ ու չգիտեմ ում ցույց տալ նկարածս: Իսկ պապիկս միշտ հետաքրքրությամբ է նայում իմ նկարչական ալբոմները և խելացի խորհուրդներ է տալիս: Նոր տարուն միշտ սպասում եմ պապիկիս գալուն: Ինքը ինձ փոխարինում է այն Ձմեռ պապիկին, ում ես թողել եմ իմ մանկության քաղցր հուշերում:

Մտքերը՝ Մանան Ավագյանի

Ես եմ
Պատուհան

3. Կարդալ  Զահրատի բանաստեղծությունները, ընտրել մեկը, ձայնագրել կամ տեսագրել։ 

4. Առաջին ուսումնական շրջանի հաշվետվություն։ Պատումի տեսքով ներկայացրե՛ք ՝

• Ձեր ձեռբերումները, հաջողությունները, դժվարությունները, 
• Հաջողված նախագծերը, ինչո՞ւ եք համարում հաջողված,
• Ձեր գրած ամենագեղեցիկ շարադրությունը, 
• Չորս ամսվա ընթացքում կարդացած ամենահետաքրքիր գիրքը, ստեղծագործությունը, 
• Ի՞նչ սովորեցի, ինչն եմ կարևորում ,
• Ձեր առաջարկները երրորդ ուսումնական շրջանի համար,
• Այլ։ 

Երկու տարի առցանց սովորելուց հետո, այժմ ես դպրոց եմ հաճախում և սովորել եմ գորգագործություն, ինչը ինձ համար մեծ հաջողություն է: Այս ընթացքում ես նաև ընթերցել եմ հետաքրքիր գրքեր, որոնք մեծ ազդեցություն են ունեցել ինձ վրա:Իմ հաջողակ նախագծերը շատ տարբեր են, բայց ես համարում եմ, որ ցանկացած նախագծ, որ ես եմ անում, հաջողակ է, քանի որ ես եմ իրականացնում: Շարադրություն գրելն էլ իմ սիրած զբաղմունքներից է, և իմ համար յուրաքանչյուր շարադրություն գեղեցիկ է, եթե այն ես եմ գրում, քանի որ ստեղծագործում եմ արդեն ութ տարեկանից: Կարեւորում եմ եւ նյութական եւ հոգեւոր արժեքները, նաեւ հումորը մարդու մեջ, խելացի լինելը եւ այլն:

5. Անհատական նախագծերի հաշվետվություն։ Ամփոփել և ներկայացնել չորս ամսվա արդյունքները՝ հղումներով։ 

Անհատական նախագծերս ՝

Դեկտեմբերի 16-20

Սիրելի՛ ընկերներ, այս շաբաթ ներկայացնելու եք ,, Մկանային համակարգ,,։ Դասրանում կներկայացնեք այս թեման և տեղում կամփոփենք դեկտեմբեր ամիսը․

• Մկանային համակարգ— դասագիրք էջ՝ 74
• Լրացուցիչ նյութ

Լրացուցիչ աշխատանք․ պատասխանել հարցերին

1.Ինչ պիսի՞ կառուցվածք ունեն կմախքային մկանները:

Յուրաքանչյուր մկանաթել ունի լայնակի շերտավոր կառուցվածք, որը պայմանավորված է նրա մեջ գտնվող հարյուրավոր սպիտակուցային թելերի`միոֆիբրիլների  որոշակի դասավորությամբ։ Մկանաթելերի խրցերում լայնակի շերտավորությունն ավելի է ընդգծվում, որի համար ստացել են միջաձիգ զոլավոր մկան անունը։ Յուրաքանչյուր մկանին մոտենում են զգացող և շարժիչ նյարդաթելեր։ Մկաններն իրենց ծայրերի ջլերով ամրանում են ոսկրերին։ Որոշ դեպքերում ջլերը ներհյուսվում են մաշկի մեջ (դիմախաղի մկաններ)։ Ջիլը կազմված է ներդակազմ շարակցական հյուսվածքից, չի կծկվում և դիմանում է մեծ ծանրության: 

2. Ի՞նչ դեր է կա տարում մկանային համակարգը:

Միջաձիգ զոլավոր մկանների դերն օրգանիզմում բազմազան է։ Նրանք մասնակցում են մարմնի խոռոչների և օրգանների պատերի կազմությանը (կրծքի, որովայնի խոռոչ, ըմպան, կոկորդ) ապահովում են մարմնի կեցվածքը, հավասարակշռությունը, ձայնի առաջացումը։ Միջաձիգ զոլավոր մկանները մասնակցում են շնչառական և կլլման շարժումներին, ձևավորում են դիմախաղը, ապահովում ակնաշարժ և ծամիչ ապարատի գործունեությունը։ Նրանց կծկումը կմախքի հետ միասին ապահովում է մարմնի տեղափոխությունը տարածության մեջ, ջերմության առաջացումը։

3.Ի նչպե՞ս են կատարվում շարժուﬓերը հոդերի ﬕջոցով:

Ձեռքերի և ոտքերի հոդերը սինովիալ տեսակի են, որը նշանակում է, որ այս հոդերում կա հեղուկ (սինովիալ հեղուկ), որը հեշտացնում է ոսկրերի շարժումները: 

Ողնաշարի և կոնքի ոսկրերն աճառային են, որոնք ավելի քիչ շարժուն են, սակայն ապահովում են լրացուցիչ կայունություն:

Կան նաև ֆիբրոզ հոդեր, որոնք լիարժեք անշարժ են և պարզապես ապահովում են կայունություն: Ֆիբրոզ հոդեր կան ձեր գանգում:

4.Որտե՞ղ են տեղակայված հարթ և ﬕջաձիգ զոլավոր մկանները:

Նրանք մասնակցում են մարմնի խոռոչների և օրգանների պատերի կազմությանը ապահովում են մարմնի կեցվածքը, հավասարակշռությունը, ձայնի առաջացումը։ Միջաձիգ զոլավոր մկանները մասնակցում են շնչառական և կլլման շարժումներին, ձևավորում են դիմախաղը, ապահովում ակնաշարժ և ծամիչ ապարատի գործունեությունը։ Նրանց կծկումը կմախքի հետ միասին ապահովում է մարմնի տեղափոխությունը տարածության մեջ, ջերմության առաջացումը։

5.Ի նչպիսի՞ հիﬓական մկանախմբեր գիտեք:

Ըստ տեղադրվածության և ֆունկցիայի մեր մարմնի մկանները բաժանվում են հետևյալ խմբերի՝ գլխի, մեջքի, կրծքի, որովայնի և վերջույթների։

Թեմա՝ Օրինաչափություն 

Ինչ է օրինաչափությունը

ցանկացած կանոնավոր կրկնվող դասավորություն, հատկապես դիզայն, որը պատրաստված է մակերեսի վրա կրկնվող գծերից, ձևերից կամ գույներից

Կաղապարը օրինաչափություն է աշխարհում, մարդու կողմից ստեղծված դիզայնի, կամ վերացական գաղափարների մեջ։ Որպես այդպիսին, օրինաչափության տարրերը կրկնվում են կանխատեսելի կերպով: Երկրաչափական նախշը մի տեսակ նախշ է, որը ձևավորվում է երկրաչափական ձևերից և սովորաբար կրկնվում է պաստառի ձևավորման նման:

Կաղապարների տարբեր օրինակներ

Զգայարաններից որևէ մեկը կարող է ուղղակիորեն դիտարկել օրինաչափությունները: Ընդհակառակը, գիտության , մաթեմատիկայի կամ լեզվի վերացական օրինաչափությունները կարող են դիտվել միայն վերլուծության միջոցով: Ուղիղ դիտարկումը գործնականում նշանակում է տեսողական նախշեր տեսնել, որոնք տարածված են բնության մեջ և արվեստում։ Կաղապարներն ունեն հիմքում ընկած մաթեմատիկական կառուցվածքը: ​Նմանապես գիտություններում տեսությունները բացատրում և կանխատեսում են օրինաչափություններ աշխարհում։

Կաղապարների տարբեր օրինակներ՝

Դեկորատիվ արվեստի շատ ոլորտներում ՝ կերամիկայից և տեքստիլից մինչև պաստառ , «նախշը» օգտագործվում է դեկորատիվ ձևավորման համար, որը արտադրվում է, հավանաբար, շատ տարբեր ձևերի առարկաների համար: Արվեստում և ճարտարապետության մեջ դեկորացիաները կամ վիզուալ մոտիվները կարող են համակցվել և կրկնվել՝ ձևավորելով նախշեր, որոնք նախատեսված են դիտողի վրա ընտրված ազդեցություն ունենալու համար:

Օրինաչափությունը բնության մեջ

Բնության մեջտեսողական օրինաչափությունները հաճախ քաոսային են , հազվադեպ են կրկնվում : Բնությունը տալիս է բազմաթիվ տեսակի օրինաչափությունների օրինակներ, այդ թվում՝ համաչափություններ , ծառեր և այլ կառուցվածքներ՝  ֆրակտալ չափսերով, պարույրներ , ոլորաններ , ալիքներ , փրփուրներ , սալիկապատեր , ճեղքեր և շերտեր:

Արդյոք դեժավյուն օրինաչափություն է ՝

Երբ ասացի օրինաչափություն եւ օգտագործեցի կրկնություն բառը հիշեցի Դեժավյու երեւույթի մասին առաջինը եկեք բացատրեմ ՝ ինչ է դեժավյուն 

Արդեն տեսած երևույթ կամ Դեժավյու, ընկալման պրոցեսի խախտումներից մեկը, որի դեպքում մարդուն թվում է, որ իբր անցյալում ինքը արդեն գտնվել է նման իրադրության մեջ, որտեղ այժմ նա հայտնվել է։

Արդեն տեսած, դեժավյու կամ դեժա վու վիճակ է, որի ընթացքում մարդը զգում է, որ նա արդեն մի ինչոր ժամանակ առաջ եղել է նման իրավիճակում, նմանատիպ վայրում, սակայն, այս զգացումը կապ չունի անցյալի կոնկրետ պահի հետ, այլ այն վերաբերվում է անցյալին առ հասարակ։ Այս տերմինը առաջին անգամ օգտագործվել է Էմիլ Բուստակի (1851 1917) կողմից՝ «հոգեբանական գիտությունների ապագան» գրքում։

Դեժավյու կարելի է զգալ արդեն վերապրած կամ արդեն փորձարկած, արդեն լսած, արդեն մտածված, արդեն արած, արդեն իմացած, արդեն ցանկացած, արդեն պատմված, արդեն փորձված։

Նաեւ դեժավյուն բավականին տարածված երևույթ է։ Հետազոտությունները ցույց են տալիս, որ մարդկանց 97% գոնե կյանքում մեկ անգամ ունեցել է այս զգացումը։

Պատճառները

Որոշ դեպքերում դեժավյուն կարելի է բացատրել երազներով, այսինքն՝ ծանոթ իրավիճակներով, որոնք իրականում տեղի չեն ունեցել, սակայն ինչ որ նման բան եղել է երազում։ 

Նաեւ կա ենթադրություն, որ դեժավյուն կարող է լինել այդպես կոչված «մասնատված ընկալունակության» հետ, երբ զգայական օրգաններից եկող ազդակները մեր ուղեղը ստանում է ոչ թե մեկ անգամ, այլ երկու անգամ, որոշակի ձգձգումով, որը կարող է թեեւ մեկ միլիվայրկյան։ Ու երբ այդ ազդակները չեն սինխրոնանում ինչպես որ հարկն է, ուղեը երկրորդ ազդակը ընկալում է որպես առաջին ազդակ։

Որպես ամփոփոմ ցանկանում եմ ասել, որ գիտական մոտեցում, որ դեժավյուն օրինաչափություն է ՝ չկա, այս թեման դեռ շատ լավ ուսումնասիրված չէ եւ ոչ մի հստակ փաստ չկա կապված դեժավյու երեւույթի մասին :

Սոփեստներ՝

Սոփեստներ ՝ մեր թվարկությունից առաջ 5-4-րդ դարերի հունական փիլիսոփաներ՝ իմաստության և պերճախոսության պրոֆեսիոնալ ուսուցիչներ, ովքեր առաջինն սկսեցին իմաստասիրություն ուսուցանել փողով։ Այսպես կոչված ավագ սոփեստ էին Պրոտագորասը, Գորգիասը, Հիպիասը, Պրոդիկոսը, Անտիփոնը,  և ուրիշներ, կրտսեր սոփեստներ՝ Կրիտիասը, Ալկիդամասը, Էվթիդեմոսը, Լիկոփրոնը, Թրասիմաքոսը, Հիպոդամոսը, Պոլոսը և ուրիշներ։ Իրենց փիլիսոփայական հայացքներով և հասարակական-քաղաքական կողմնորոշմամբ սոփեստները միասնական ուղղություն չէին կազմում։ Սոփեստների փիլիսոփայական հետաքրքրությունների ծանրության կենտրոնը բնափլիսոփայությունից փոխադրեցին բարոյականության քաղաքականության, հռետորության, այդ ուղիով՝ խոսքի ու մտածողության կառուցվածքի, առհասարակ իմացաբանության հարցերի ոլորտը, և դա նրանց պատմական ծառայությունն է։

Առաջադրանքներ ինքնուրույն աշխատելու համար/կատարել տանը և վերլուծությւոնը տեղադրել բլոգում։

1. Ինքնուրույն վերլուծել հետևյալ սոփեստությունը.

Յոթ ընկերներ սրճարանում սեղան էին պատվիրել։ Բայց թյուրիմացություն էր տեղի ունեցել. սեղան էին պատրաստել վեց հոգու համար, իսկ սրճարանի սրահը լեփ-լեցուն էր։
Այնուամենայնիվ, մատուցողը գտավ ելքը։
Առաջին հյուրին նա նստեցրեց առաջին աթոռին, իսկ նրա կողքին՝ նույն աթոռին, խնդրեց ժամանակավորապես նստել նրա ընկերուհուն։ Երրորդին նա նստեցրեց առաջին երկուսի կողքի աթոռին, չորրորդին՝ հաջորդ աթոռին։ Հինգերորդին նա նստեցրեց առաջին երկուսի դիմաց, վեցերորդին՝ նրա կողքի աթոռին։ Եվ վերջապես, ազատ մնացած վեցերորդ տեղում նա նստեցրեց առաջին հյուրի ընկերուհուն։ Ինչպե՞ս ստացվեց, որ յոթ հոգին տեղավորվեցին վեց աթոռի վրա։

Երկու հյուրին նստեցրեց նույն աթոռին։

Հոկտեմբերի 7-ից հոկտեմբերի 11-ը

Սիրելի՛ սովորողներ, միասին կարդում և լուծում ենք տրամաբանական խնդիրներ։

Դասի վերջին 10 րոպեն տրամադրում ենք Kahoot.it հարթակով ստեղծված խաղին։ 

Խնդիր 1:
Անուշը ունի 5 տարբեր թիվ և դրանք հաջորդական թվեր չեն։ Առաջին թիվը մեծ է երկրորդից, երկրորդը մեծ է երրորդից, իսկ չորրորդ թիվը փոքր է հինգերորդից և մեծ է երրորդից: Ո՞րն է ամենափոքր հնարավոր թիվը:

փոքր է 3 

Խնդիր2:
Յուրաքանչյուր 10-րդ փուչիկը պայթում է: Եթե դուք փչում եք 100 փուչիկ, ապա քանի՞ փուչիկ կպայթի, մինչև բոլորը փչված լինեն:

100:10=10 

Խնդիր 3:
Երկու գնացք շարժվում են միմյանց ընդառաջ՝ նույն արագությամբ։ Նրանց միջև հեռավորությունը 100 կմ է։ Ծիծեռնակը թռչում է առաջին գնացքից դեպի երկրորդը և վերադառնում  է առաջին գնացքին: Եթե ծիծեռնակը թռչում է 50 կմ/ժ արագությամբ, ապա քանի՞ կիլոմետր է այն անցնում մինչև գնացքները հանդիպելը։

50

Խնդիր 4:
Կա 5 քաղաք, որոնք պետք է կապել ճանապարհներով այնպես, որ յուրաքանչյուր քաղաքը կապվի մյուս չորս քաղաքների հետ: Քանի՞ ճանապարհ է անհրաժեշտ:

10

Խնդիր 5
Անուշն ունի այգի, որտեղ տարբեր տեսակի ծաղիկներ կան՝ կարմիր, դեղին, և կապույտ: Ամեն օր նա ընտրում է երեք ծաղիկ՝ մեկը ամեն տեսակից: Երրորդ օրը նա տեսնում է, որ իր բոլոր հնարավոր ընտրությունները կատարել է: Քանի՞ ծաղիկ ունի Անուշը:

Խնդիր 6

30 սովորողները պետք է մասնակցեն երգչախմբի և թատրոնի խմբակի պարապմունքներին։ Յուրաքանչյուր սովորող կարող է ընտրել կամ երգչախմբում, կամ թատրոնում մասնակցելու հնարավորությունը։ Եթե 15 սովորողները ընտրում են և մասնակցում երգչախմբի պարապմունքին, այս դեպքում քանիսն են կարողանում ընտրել և մասնակցել թատրոնի խմբակի պարապմունքներին։ Նույն սովորողը չի կարող մասնակցել երկու խմբակի պարապմունքներին։

Խնդիր 7

4 բադն ու 1 սագը միասին կշռում են 4կգ 100գ, իսկ 5 բադը և 4 սագը միասին՝ 4 կգ են։ Քանի՞ կգ է 1 բադը։

Խնդիր 8

Գծի՛ր 3 ուղիղ և նրանց վրա տեղադրի՛ր 3 կետ այնպես, որ ամեն ուղղի վրա լինի 2 կետ։

Խնդիր 9

Եռանկյան վրա տեղադրված շրջանների մեջ 1-ից 9 թվանշանները տեղադրել այնպես, որ յուրաքանչյուր կողմում նշված թվանշանների գումարը նույնը լինի։ Այդ նույն կողմերի գումարի քառակուսիները նույնպես պետք է նույնը լինեն։

Հոկտեմբերի 14-ից 18-ը

Սիրելի՛ սովորողներ, այս շաբաթվա ընթացքում միասին կարդում և լուծում ենք տրամաբանական, անսովոր լուծումներ պահանջող խնդիրներ։ Խնդիրների մի մասն՝ այստե՛ղ։

Մաթեմատիկական խաղեր — 14-18․10․2024Download

Խնդի՛ր 1

Գտի՛ ր այնպիսի քառանիշ թիվը, որը գրելուց հետո այն շրջելով նորից կստանաս նույն քառանիշ թիվը։

1961

Խնդիր 2

Աննան գրեց 1 թիվը, հետո  հաշվեց «один» բառի տառերի քանակը և գրեց 4: Այնուհետև գրեց «четыре» բառի տառերի քանակը՝ 6 և այսպես շարունակ։ Ի՞նչ թիվ պետք է գրել շարքի 100-րդ տեղում։

Պատասխան ՝ 5 

Խնդիր 3

Նկարում երևում է թվային երկու սյունակ։ Երկրորդ սյունակը ստացվել է առաջին սյունակում գրված թվերի հակառակ դասավորությունից և տեղադրվել է։ Առանց գումարման գործողության կատարման կարո՞ղ եք գտնել, թե արդյո՞ք սյունակների թվերի գումարը հավասար են։

Այո հավասար են :

Խնդիր 4

Ութ միանմնան աղյուսներից պատրաստել են զուգահեռանիստ։ Աղյուսի չափումներից մեկը տրված է 3: Ինչի՞ է հավասար մեկ աղյուսի ծավալը։

Պատասախան ՝ 225

Առաջին խնդիր

1. Հարց: Անհրաժեշտ է որոշել, թե որ պարանն անհնար է կտրել, առանց այն քանդելու:

Լուծում: Հարկավոր է պարզել, թե որ պատկերը հնարավոր չէ ուղղել և դարձնել պարզ շարանը, առանց դրա որևէ մասը կտրելու: Ընտրությունը կախված է նրանից, թե յուրաքանչյուր պատկերի հանգույցները որքանով են կապված:

Պատասխան:B տարբերակն ունի տիպիկ հանգույց, որը չի քանդվում առանց կտրվելու:

Երկրորդ խնդիր

2. Հարց: Հարկավոր է ընտրել այն բազմանկյունը, որը կավելացնի հինգանկյուններին այնպես, որ ստացվեն երկու փակված շրջանագծեր:

Լուծում: Պատկերում ցույց է տրված տարբեր բազմանկյուններ, որոնցից մեկը ճիշտ ձևով կլրացնի հինգանկյունները, որպեսզի ստացվի երկկողմանի կապ:

Պատասխան: E տարբերակը ստեղծում է անհրաժեշտ կապը:

Երրորդ խնդիր

3. Հարց: Երկրորդ պատկերում երկկողմանի եռանկյուններ ավելացնելուց հետո, ինչքան տոկոսով է մեծանում տարված առաջին պատկերի մակերեսը:

Լուծում: Երկրորդ պատկերում նշված է, որ երկու եռանկյունների ավելացումը մեծացնում է մակերեսը որոշակի տոկոսով: Հարկավոր է հաշվարկել հավելավճար մակերեսը:

Պատասխան: C50% մակերեսի ավելացում է ստացվում:

Չորրորդ խնդիր

4. Հարց: Գտնել՝ ինչ է ցույց տալիս  \frac{20 \times 24}{2 \times 0 + 2 \times 4}  արտահայտությունը:

Պատասխան: D — 60

Հինգերորդ խնդիր

5. Հարց: Քառանկյուններից կտրելով տետրադրի յուրաքանչյուր գագաթը՝ քանի՞ անկյուն է ստացվում:

Լուծում: Տետրադրի յուրաքանչյուր անկյուն կտրելիս ստացվում է նոր գագաթ, այնպես որ գագաթների քանակը մեծանում է:

Պատասխան: D 12 անկյուն է ստացվում:

Վեցերորդ խնդիր

6. Հարց: Մանեն ունի թվանշաններ 1, 5 և 11 և ցանկանում է ստանալ չորսանիշ թիվ: Քանի՞ տարբեր չորսանիշ թիվ կարող է ստացվել:

Լուծում: Որպեսզի ստանանք չորսանիշ թվեր՝ պետք է հաշվել տեղադրությունների քանակը: Կան 3^4 = 81 բոլոր հնարավորությունները:

Պատասխան: B 4 :

Ըստ գծագրերի տվյալների գտնել x-ը.

ա)

360 — 232 = 128,
x = 128 : 2 = 64:

բ)

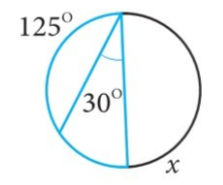
125 + 60 = 185,
x = 360 — 185 = 175:

գ)

180 + 112 = 292,
x = 360 — 292 = 68,
x = 68:2 = 34:

դ)

215 + 40 = 255,
x = 360 — 255 = 105:

2)AB կիսաշրջանագծի վրա վերցված են C և D կետերն այնպես, որ

∪AC = 57°∪BD = 63°Շրջանագծի շառավիղը 12 սմ է:

∪AC=57^o, ∪BD=63^o   

Գտեք CD լարը, եթե շրջանագծի շառավիղը 12 սմ է։

3)AOB կենտրոնային անկյունը 30^o -ով մեծ է AB աղեղին հենված ներգծյալ անկյունից։ Գտեք այդ անկյուններից յուրաքանչյուրը։

Կենտրոնական անկյունները
Շրջանագծի կենտրոնից OOO դեպի AAA, BBB, CCC և DDD կետերը ձգված շառավիղներն են։ Այսինքն, ∠AOB\angle AOB∠AOB և ∠COD\angle COD∠COD կենտրոնական անկյուններն են, որոնք հավասար են \overarcAB\overarc{AB}\overarcAB և \overarcCD\overarc{CD}\overarcCD անկյուններին։